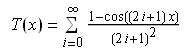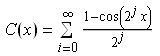For my first post on this blog, I’ve decided to stay away from complex projective 4-space, but instead write about something equally mathematical and just as interesting: pathological functions. The ideas may be more familiar to you in the form of fractals, although the definitions are different and not equivalent: a pathological function is a function from the real numbers to the real numbers, whereas a fractal curve is a subset of the plane. I’ll be discussing fractal curves more in later posts.
The ‘blancmange function’ is a famous example of a pathological function, which is everywhere continuous but nowhere differentiable. It is defined by successively summing triangle waves of exponentially decreasing size together.
Successive approximations to the blancmange function formed by adding triangle waves together
In the same way that the blancmange function is expressed as an infinite series of triangle waves, a single triangle wave can be expressed as a sum of cosine waves (and constant terms, which can be regarded as cosine waves of infinite period), known as a Fourier series. These are named after a Mr. Fourier, who realised that the sounds produced by musical instruments can be expressed as Fourier series, and by induction an entire orchestra. The triangle wave, for example, is given by the following Fourier series:
Fourier series of the triangle wave
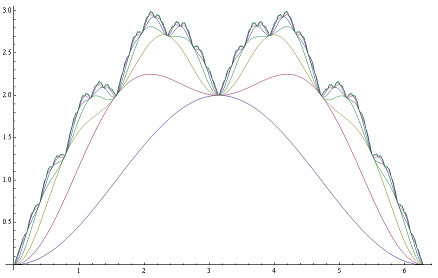
If we just take the first term of this Fourier series, and add them together as in the blancmange function, we obtain a simpler pathological function. To continue the tradition of naming pathological functions after desserts, and in honour of Trinity College, where the dessert was conceived, I have entitled this the ‘creme brulee function’. It also has a simple Fourier series:
Fourier series of the creme brulee function
It is also everywhere continuous and nowhere differentiable, like my hairstyle and the blancmange function, and greatly resembles the latter. The successive approximations are more curvaceous and aesthetically pleasing than the jagged edges of the sawtooth function.
Successive approximations of the creme brulee function
The original blancmange function can easily be expressed as an infinite sum of creme brulee functions. I’ve done it, but to save uploading another formula, I’ll leave this as an exercise to the reader. This infinite series should suggest why the creme brulee function and blancmange function differ only slightly: the second term is nine times smaller than the first term, and subsequent terms are even more negligible.