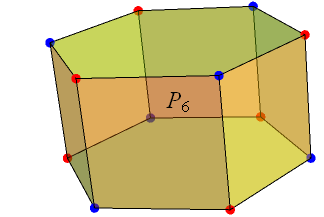
There is a plethora of polyhedra. One way to classify polyhedra is based on their symmetry, transitivity and other properties. An alternative, constructive approach, by John Conway, involves specifying sequences of operations to turn one polyhedron into another. Quite a good starting point is the hexagonal prism:
A hexagonal prism, with alternate vertices coloured red and blue.
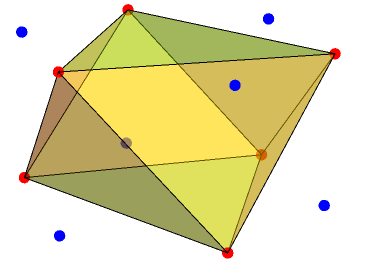
There are many operations we can apply. For this post, it suffices to consider only four: alternation, truncation, rectification and duality. We’ll begin with alternation. We 2-colour the vertices red and blue and discard all of the blue vertices. When applied to our hexagonal prism, we obtain the octahedron:
The octahedron with Conway notation lP6
This is represented ‘lP6’, as we use ‘l’ for alternation and the original solid was the hexagonal prism, P6. We’ll now truncate it using the operator ‘t’ to obtain the truncated octahedron. This is one of the more interesting Archimedean solids, being able to tile three-dimensional space.
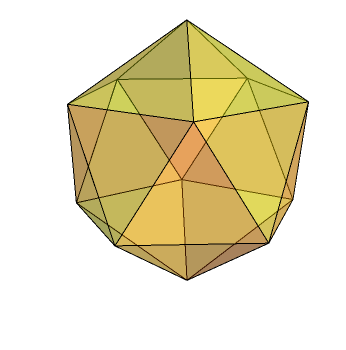
Pretty impressive, huh? Well, things are going to take a turn for the unexpected when we alternate it. See if you can guess what ltlP6 is. You should be very surprised by this. Amazed, even. Prepare for a shock unseen in your wildest dreams.
Yes, it’s an actual icosahedron.
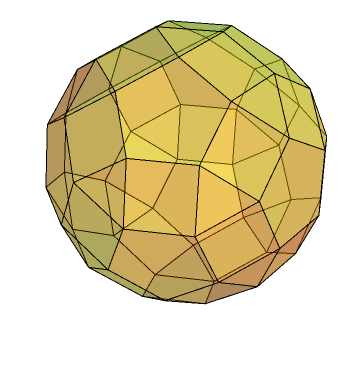
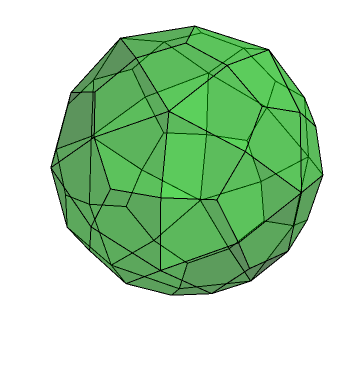
There’s a very good reason why this occurs, although the transition from octahedral to icosahedral symmetry is quite unusual. We can then apply two rounds of ‘a’ (rectification, which is an extreme version of truncation where none of the original edges remain) to obtain that most sesquipedalian of solids, the small rhombicosidodecahedron.
Rhombicosidodecahedron, aaltlP6
This is an Archimedean solid. We can then take its dual, which is a Catalan solid called the deltoidal hexecontahedron. The transition from a uniform polyhedron to a non-uniform one is signalled by the colour change:
Deltoidal hexecontahedron, daaltlP6
The duals of Archimedean solids are commonly known as Catalan polyhedra. We can get any Platonic, Archimedean or Catalan polyhedron by starting with the hexagonal prism and applying some combination of those four operations. If you include other operations such as stellation, you can obtain spiky solids like the one knitted by Katie Steckles and mentioned in my previous post. Joseph Myers also has an extensive collection of hand-made cardboard polyhedra of various types.
No polyhedra were harmed in the making of this post. If you are concerned about the welfare of polyhedra, consult your local psychiatrist.
Where do you get this “l” operation from? I can see that it selects the correct number of vertices for these two cases, but how does it actually work? Applying this operation to a truncated octahedron with regular faces will not return a regular icosahedron. If you truncate according to the golden ratio, then maybe it would work. The problem with all of the geometric operations corresponding to the Conway notation is that they are not as well defined as compass and straight edge operations.
Coloring vertices can be useful for analysing a symmetry group, but it really only helps with transformation in a few rare cases. Lots of shapes such as the tetrahedron, the octahedron, could not be transformed by “l”. The cube and the dodecahedron are two notable exceptions where a subset of the vertices bound a nice shape.
I actually have a Mathematica code for transforming Polyhedra using Conway Notation. It needs some more work done. Feel free to contact me regarding this project or anything else.
Brad
It’s a well-known geometric operation called ‘alternation’, which doesn’t appear to be in the standard Conway notation. It only works if the graph of vertices and edges is 2-colourable. Choose an arbitrary vertex and colour it red. Colour all adjacent vertices blue. For each blue vertex, colour all adjacent vertices red, and vice-versa. Iterate until every vertex is coloured. Now, you have a choice: you can select the convex hull of either the red vertices or the blue vertices. Typically, but not always, these will be chiral enantiomorphs. We have the identity sX = ltaX, where ‘s’ is the snub operator.
You’re correct in the realisation that truncating an octahedron according to the golden ratio will give the same arrangement of vertices as two icosahedra. An icosahedron has a vertex located at each cyclic permutation of (±1,±phi,0); an appropriately truncated octahedron has vertices at all permutations, not just cyclic ones.
Your argument also applies to the ‘truncated icosidodecahedron’. An actual truncation of the uniform icosidodecahedron does not result in a uniform truncated icosidodecahedron; instead of squares, we have golden rectangles. These complications are avoided by considering polyhedra from a topological perspective, rather than a geometric one.
I agree with you: this ‘alternation’ is an operator with limited use, because the number of vertices of every face must be even. Moreover it is not proposed by Conway. I programmed also the Conway Polyhedron Notation in Mathematica. I am interested how you get along with ‘gyro’. I have quite a bit of problems in finding a stable solution.
Lei Willems
Pingback: The Betts problem | Complex Projective 4-Space
Pingback: Johnson solids | Complex Projective 4-Space
Is there a transition solid between Octahedron to Dodecahedron (like Cuboctohedron between Cube and Octahedron)? Or can you make a truncated transition? Do you have to use a compound and is there one? There must be a logical progression or are they worlds apart by their different symmetries?