Studies have shown that bilateral symmetry in female humans is linked to attractiveness. Also connected with attractiveness is the presence of the golden ratio (the positive real root of the quadratic equation x² – x – 1 = 0, approximately 1.618034). Earlier, we saw how it determines the arrangement of primordia in a Helianthus sunflower. It is far more ubiquitous than that, occurring in the proportions of the Parthenon, the position of the naval and, thanks to recent research by a Belgian gynaecologist, the dimensions of the uterus.
One must be careful to avoid seeing phi where it doesn’t actually exist. It’s very easy to read too much into a set of data, and there are (probably justified) claims that the Belgian gynaecologist did just that. However, certain mathematical objects undeniably feature the golden ratio. A regular pentagon is one of those — the ratio between the length of a diagonal and the side length is equal to phi.
Obviously these are necessary, but by no means sufficient, conditions for attractiveness: starfish intrinsically incorporate the golden ratio and display five axes of bilateral symmetry, but we do not find them attractive (at least I don’t, and I hope the same applies to you). A sufficiently-old-to-be-copyright-free drawing of these echinoderms is given below:
Nevertheless, we can do better than that. There are amoeboids called Radiolaria, some of which have icosahedral symmetry. So do, in fact, viruses such as the common cold. The symmetry enables the viruses to be specified by a short description: a single gene can code for 60 identical proteins forming the shell of the virus. A regular icosahedron has six axes of pentagonal symmetry.
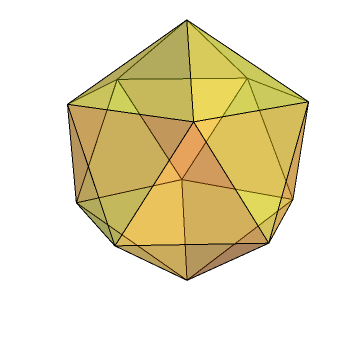
An icosahedron has a rotation group of order 60, so can be split into 60 congruent pieces. By specifying just one of these identical pieces, a virus can encode its shell in an impressively compact sequence of DNA.
If, like the inhabitants of Edwin Abbott’s Flatland, there is a spatial dimension beyond our own, then there may be organisms with hyper-icosahedral symmetry. In four dimensions, there are regular polychora called the 120-cell and 600-cell, which are four-dimensional analogues of the dodecahedron and icosahedron, respectively. There is even such a sadistic puzzle as a Rubik’s 120-cell, which so far has only been solved by six people. Beyond four dimensions, however, there are no further interesting regular polytopes; only simplexes, hypercubes and their duals exist in five or more dimensions.

Pingback: Projective polyhedra | Complex Projective 4-Space