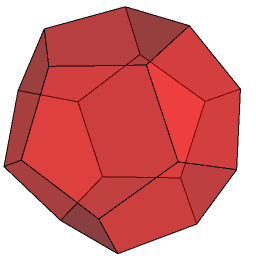
The Platonic solids can be regarded as regular tilings of the surface of a sphere in much the same way as the square, hexagonal and triangular tilings of the plane are regular. For example, the dodecahedron is a tiling of the sphere with twelve pentagons.
If you read the ‘Projective geometry‘ chapter of MODA, you will see that the points on the projective plane can be identified with the lines through the origin or, equivalently, pairs of antipodal points on a sphere. So, we can identify opposite points on our dodecahedron as being ‘the same thing’. An advantage of this is that the visible half of the dodecahedron is the entire tiling of the projective plane:
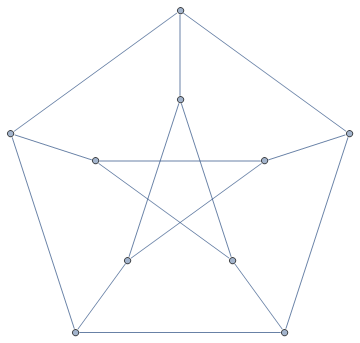
This has 6 faces, 10 vertices and 15 edges, compared with the dodecahedron’s 12, 20 and 30, respectively. Hence, this tiling of the projective plane is called the hemi-dodecahedron. If we form the vertex/edge graph of the hemi-dodecahedron, the result is the rather famous Petersen graph:
Even though it can be drawn on the projective plane, it cannot be realised on the plane without edges crossing (as above). This is because it contains the complete graph K5 as a graph minor. The Petersen graph is really interesting in its own right, with Donald Knuth commenting that it is almost always a counter-example to false conjectures about graphs!
Returning to projective polyhedra, we can also construct its dual, the hemi-icosahedron. It is a remarkable fact that 11 hemi-icosahedra can be stitched together to form an abstract self-dual polytope, and likewise 57 hemi-dodecahedra constitute the 57-cell. In the same vein as the Rubik’s 120-cell mentioned earlier, Nan Ma recently designed a web applet for exploring a Rubik’s 11-cell. As far as I know, the same hasn’t yet been done for the 57-cell.
Quickly reading the Planar graphs section of Combinatorics II (third chapter of MODA), you’ll see how certain tilings such as the Klein quartic can be obtained by ‘rolling up’ finite patches of infinite tilings. The 11-cell and 57-cell are rolled up patches of the icosahedral and dodecahedral honeycombs, respectively. Claudio Rocchini rendered a really pretty stereographic projection of the former:
Hyperbolic honeycombs are the three-dimensional cousins of the tilings used in the Circle Limit paintings. Instead of the infinite variety in two dimensions, however, there are only four regular hyperbolic honeycombs.



Pingback: Outer automorphism of S6 | Complex Projective 4-Space
Pingback: Ten things you (possibly) didn’t know about the Petersen graph | Complex Projective 4-Space
Pingback: Descartes snark | Complex Projective 4-Space
Evaluation results could be reported to show the estimated proportion of the inhabitants or subpopulation that answered every item and process correctly https://math-problem-solver.com/ .
Positive, we are surrounded by seemingly overwhelming day by day
experience that the world is flat.