Combinatorial cake

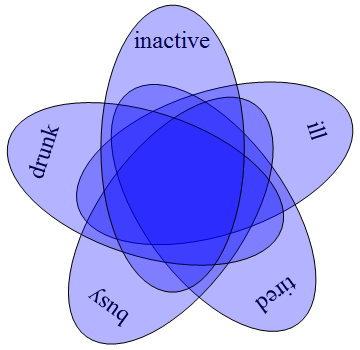
Forgive me if there is a slight lapse in the frequency of CP4space postings. You can attribute it to me lying in the quintuple-intersection of the following Venn diagram:

This particular arrangement of ellipses partitioning the plane into 32 connected subsets was discovered by Branko Grunbaum, who you may recognise as one of the authors of Tilings and Patterns. There have been similarly symmetrical Venn diagrams discovered with seven and eleven sets, but they require much more convoluted curves than mere ellipses. The article claims that they can only exist for prime numbers of sets. I doubt this assertion, since the obvious argument (that n divides 2^n – 2, which follows from the symmetry of the configuration) does not rule out Fermat pseudoprimes such as 1729.

Speaking of symmetrical objects, there was some recent hype about hexaflexagons. They were originally mentioned in an article by Martin Gardner some years ago, then discussed ad nauseam in three videos by Vi Hart. If you didn’t already know, Vi Hart is one of a group of rebellious rapscallions attempting to overthrow accepted mathematical notation by using the symbol τ = 2π. (This reminds one of when Royal Mail wasted millions of pounds changing its name to Consignia, only to revert shortly afterwards.)

[youtube=http://www.youtube.com/watch?v=jG7vhMMXagQ]

Don’t let her attempt to convert you to Tauism with those Raspberry Pies! Instead, take a look at this much more delectable dessert I conceived earlier.

This, of course, was consumed months ago by a select group of really fortunate people. You may recognise it as an attempt to reconstruct the infamous Wolfson building, a monstrosity erected in the 1960s. It even comes with its own ‘suicide door’, which faces out of a second-floor window into thin air!

Yes, this actually exists. You may have noticed from the cake and the photograph that this building is an orthogonal polyhedron. If you haven’t heard the terminology before, it’s just a polyhedron where all incident edges are perpendicular. There are some nice combinatorial problems on this theme.

The plane partition problem

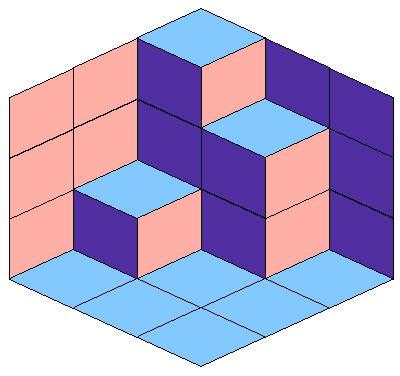
A plane partition is an orthogonal polyhedron composed of unit cubes, such that there are no empty spaces below, behind or to the left of each cube. For instance, this is a valid plane partition:

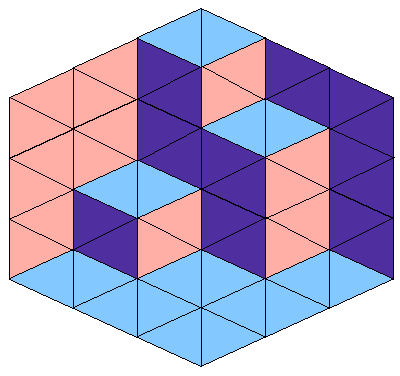
How many plane partitions can fit inside a cube of side length n? It is a remarkable fact that drawing it in the isometric projection actually converts it into a seemingly different problem. Here is the same polyhedron drawn inside the 3 × 3 × 3 cube (i.e. the case where n = 3).

On second glance, this is also a tiling of a hexagon of side length 3 with rhombi! Regarding each rhombus as the union of two triangles, this can be rephrased as a bipartite matching of the following grid of triangles:

Observe that the triangles are either ‘pointing left’ or ‘pointing right’, and adjacent triangles point in opposite directions. We will thus categorise the triangles into two sets, L and R. Observe also that there are equal numbers of rhombi of each colour. This will prove useful later on.

Form an adjacency matrix, where each row corresponds to a triangle in R and each column corresponds to a triangle in L. Each element of the matrix is either 1 (if the triangles corresponding to the row and column are adjacent) or 0 (otherwise). The determinant of this matrix counts the ways in which we can biject elements in L to elements in R, respecting adjacency. So, this determinant counts precisely the number of tilings of the hexagon with rhombi, and thus the number of plane partitions!

More things on this theme are described in this article by the AMS. For instance, the problem of finding domino tilings of a chessboard is solved almost identically.