Let’s consider the group S6 of permutations of {1,2,3,4,5,6}. For fairly boring reasons, we can find S5 living inside there — the subgroup which fixes the element ‘6’. More generally, S(n-1) is contained within Sn.
S6 is special, though, since there’s actually a well-disguised S5 hiding in there, which isn’t obvious at all. One way of proving its existence is actually to find it, by writing down a subgroup consisting of 120 permutations and showing that it’s isomorphic to S5. However, that’s ugly, uninsightful and unworthy of inclusion here. Fortunately, there are more elegant ways to see what’s going on:
The Elliott configuration
The Elliott configuration (above) is a colouring of K6 we explored when finding five-dimensional and four-dimensional Bettsian sets with no symmetry. Indeed, it is not difficult to show that the colouring of the graph above renders it asymmetrical. However, if we allow colours to be permuted, we suddenly acquire a large bunch of symmetries.
Label the vertices A,B,C,D,E,F from top-left clockwise. We can reflect in the vertical axis, i.e. permuting the vertices with (AB)(CF)(DE) in cycle notation, to transpose the colours red and yellow. Similarly, the 5-cycle (ACFED) leaving B fixed causes the five colours to be cycled (blue → green → yellow → red → purple). This is sufficient to show that any permutation of the colours can be obtained by permuting the vertices, and this permutation is uniquely determined (by asymmetry!).
In other words, we have a group isomorphic to S5 (permutations of five objects) sitting inside S6 (permutations of six objects) as a subgroup, but not in the trivial way. An immediate corollary is that we can also find a non-trivial A5 hiding inside A6, which has a couple of other elegant constructions:
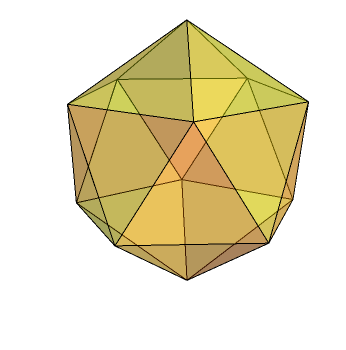
Rotations of an icosahedron
Consider the six ‘diameters’ of an icosahedron. Every rotational symmetry causes the diameters to be permuted, so the rotational symmetry group (isomorphic to A5) lies inside S6 in a non-trivial way. These permutations of diameters are actually all even permutations, so we get the stronger result that A5 inhabits A6.
To see that the rotational symmetry group of an icosahedron is indeed A5, consider the centres of each of the triangular faces. They can be partitioned into five sets of four points, with each set describing a regular tetrahedron. The rotational symmetries of the icosahedron correspond to even permutations of the five tetrahedra.
PSL(2,5)
A point on the projective line can essentially be represented as a ratio. Over the finite field F5, there are six such ratios, namely 0/1, 1/1, 2/1, 3/1, 4/1 and 1/0. The group of projective transformations PSL(2,5) permutes these six points and is isomorphic to A5. Again, all permutations obtained in this manner are even permutations, so A5 inhabits A6 in a non-trivial way.
These projective special linear groups are quite awesome. PSL(2,7) is isomorphic to the symmetries of the Fano plane (see the end of the projective geometry chapter of MODA) and the Klein quartic. PSL(2,11) is found as a maximal subgroup in the Mathieu group M11 and as the symmetry group of the 11-cell.
Vladimir Arnold observed how exceptional objects sometimes occur in groups of three, such as PSL(2,5), PSL(2,7) and PSL(2,11). He coined the term Trinity to refer to these families, a word I highly approve of…


Pingback: Iterated Aut revisited | Complex Projective 4-Space
Pingback: MOG | Complex Projective 4-Space
Pingback: How to count the conjugates of an exotic $S_5$? - MathHub
Is there any easy way to see from the icosahedron that the inclusion of A5 into A6 extends to an inclusion of S5 into S6?
The easiest way is probably to convince yourself that the icosahedron with A5 symmetry can be easily described using points with coordinates in Q(sqrt(5)) and then to examine what happens when you replace sqrt(5) with -sqrt(5).