Unfortunately, I am currently being invaded by millions of microscopic icosahedra (at least, I hope this is the common cold). I apologise on their behalf for any slight lapse in the frequency of CP4space postings. Don’t worry; the sixth cipher was made ages ago and shall be automatically uploaded at the usual time of 00:01 GMT.
Another one of Ben and Hunter’s bizarre mathematical objects of the week was a function over two variables with a single stationary point, which is a local minimum but not a global minimum. It is difficult to envisage how this is possible (a volcano, for instance, has at least one saddle point on its rim). Counter-intuitively, the solution is actually relatively simple:
If the three-dimensional surface is difficult to visualise, then you may prefer a contour plot instead. Observe that this is an even function, i.e. f(x,y) = f(-x,-y):
Apparently, someone assumed the non-existence of such functions in a proof, and it took several hours before an example was discovered.

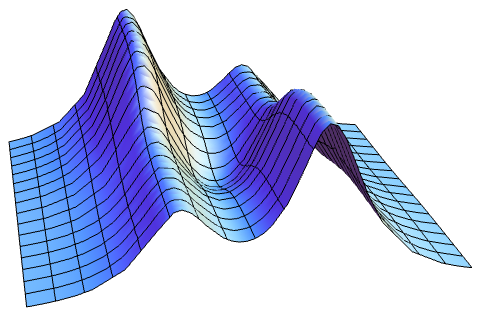

It’s still a volcano, except its rim is stretched out to infinity.
Good luck with icosahedra, get better soon…
Oh, yes, a projective volcano — I like that!
Thank you very much.