A matchstick graph is a planar graph with a plane embedding where all edges are of unit length. The name derives from the fact that they can be assembled on a flat surface out of matchsticks of equal length. Of particular interest are n-regular matchstick graphs. It’s easy to find 1-regular and 2-regular matchstick graphs (line segment and equilateral triangle, respectively). I’ll leave the case n = 3 as an exercise to the reader (it’s possible with 8 vertices and 12 edges, and not the first such graph you think of).
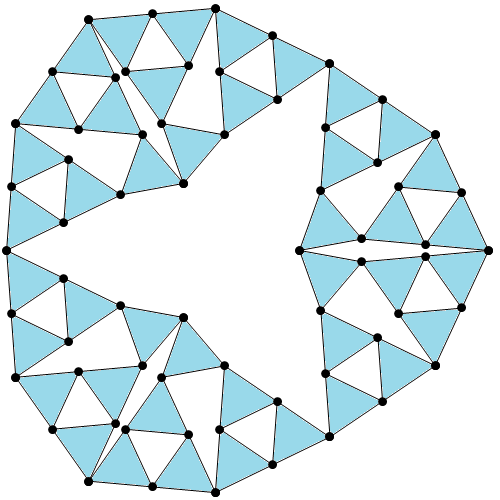
The smallest known 4-regular matchstick graph is the Harborth graph, with 52 vertices. It’s quite fun to make your own 4-regular matchstick graphs; mine ended up with 63 vertices:
This has the additional property that the edges can be partitioned into 42 triangles, where each vertex is incident with two triangles. From this, it is therefore possible to derive a 3-regular planar graph of 42 vertices; this is obtained by doing the Δ-Y transform and contracting the resulting edges. Interestingly, this graph is itself a matchstick graph!
It has been proved that there are no finite 5-regular matchstick graphs, and the only 6-regular matchstick graph is the infinite triangular tiling (proof: consider Euler’s formula). On the surface of a sphere, however, the situation is different; there are a few 5-regular examples.
The next object in this sequence is an infinite planar 5-regular matchstick graph.