Egmohedron

Partially inspired by the chiral icosahedral sculptures by George Hart and Bathsheba Grossman, I have decided to create one of my own. It’s composed of thirty identical components, each of which is a distorted lemniscate. Note that the lemniscate has a Klein 4-group of symmetries:

In principle, this could be constructed by slotting together two identical simply-connected halves, which can easily be produced by three-dimensional printing. This lemniscate can then be used as a ‘building block’ to assemble more complex configurations. For instance, the EGMO logo is composed of five of these lemniscates arranged in a symmetrical design:

It’s possible to extend this five-fold symmetry to chiral icosahedral symmetry (order 60), producing an elaborate arrangement of linked lemniscates known as the egmohedron. Now that I’ve discovered how to create animations in Mathematica, I can’t resist doing this. Sorry if it eats up your bandwidth…

If I can gain access to a 3D printer, I’ll try building an actual egmohedron. The production costs should be relatively cheap due to being composed of one unique part, which should be easily printable. I might need to revise the shape of the lemniscate to ensure that the structure is rigid.

Assuming everything goes to plan and we can make sufficiently many egmohedra in the next couple of months, it might be possible to award them as prizes to the gold medallists in EGMO 2013. I can’t guarantee anything, of course.

Group actions

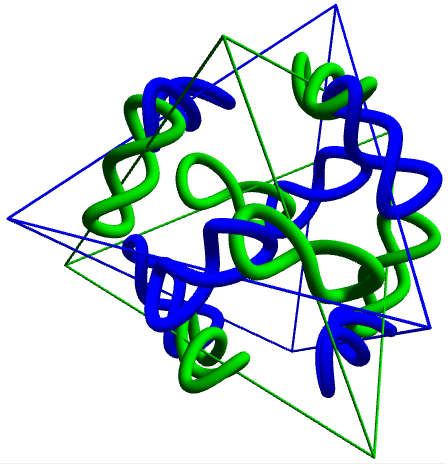
There are thirty lemniscates in total, partitioned into five sets (shown as different colours), each containing six lemniscates positioned at the vertices of an octahedron. If you consider the group action of the rotational group on these five sets, you’ll be able to observe the isomorphism I ≈ A5. The stabiliser of each set is the chiral tetrahedral group, isomorphic to A4. Skewering the lemniscates in a particular set gives a tetrahedron:

If you skewer all thirty lemniscates in the manner shown above, you’ll obtain the famous compound of five tetrahedra. Assuming my memory serves me correctly, Joseph Myers has made a cardboard model of it.

Each lemniscate is trivially equivalent to the unknot. Any two ‘adjacent’ lemniscates form a Hopf link, shown clearly in the diagram of two tetrahedra.