The torus is a reasonably interesting object. It can be embedded in as a quartic surface bounding a doughnut, or obtained by identifying opposite edges of a square. An intermediate between these constructions is the Clifford torus, which is the Cartesian product of two circles.
On the sphere, the Schönflies theorem (related to the Jordan curve theorem) tells us that any closed curve splits the surface into two components, each of which is homeomorphic to the disc. Obviously, this is not true on the torus: removing a small disc from the surface gives a surface which is not simply connected, and therefore not homeomorphic to the unit disc. More surprisingly, it is possible to remove a closed curve without creating two disjoint components. Indeed, this enables two linked loops to be drawn on a torus:
I had intuitively assumed that this was impossible (it’s hard to visualise until you see the diagram above), which caused great confusion when I read that the Petersen graph is toroidal but not linklessly embeddable. Even more impressively, the trefoil knot can be drawn on the surface of a torus:
For obvious reasons, it is known as a torus knot. Torus knots can be obtained by drawing a line of rational slope on a unit square and identifying pairs of opposite edges. The trefoil knot corresponds to the rational 3/2. Similarly, the rational 5/2 gives rise to the cinquefoil knot.
If we choose an irrational number instead, then we get an injection from the real line to a torus. For instance, here is the image of [0, 100] using the irrational number φ.
The image of the real line is a dense subset of the torus, and serves as a good counter-example for disproving certain false statements in topology.

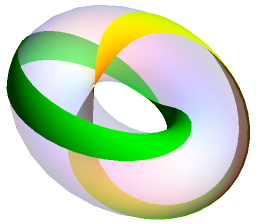


I thought Petersen graph is not linklessly embeddable. Actually, I thought it’s forbidden minor of linkless embeddings. You stated so in “Graph minors” article.
Oh, yes, when I said ‘linklessly embeddable’, I meant ‘not linklessly embeddable’. Hence, every embedding of the Petersen graph into R^3 (including one whose image is a subset of the surface of a torus) contains two linked rings, proving that there exist linked rings on the surface of a torus.
Thanks for noticing the typo; I’ve amended it now.
Pingback: First female Fields medallist | Complex Projective 4-Space
Hello There. I found your blog using msn. This is a
really well written article. I’ll make sure to bookmark it and come back to read more of your useful info.
Thanks for the post. I will definitely return.
SPAM SPAM SPAM SPAM