The Gamma function, Γ, is an extension of the factorial function to the complex plane. Specifically, Γ(n) = (n−1)! for all positive integers n. It is defined, more generally, by analytic continuation of the following integral, which converges for all complex numbers with positive real part:
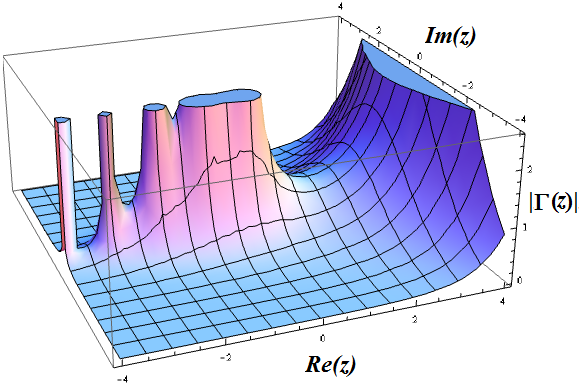
The factorial identity can be verified using integration by parts. Specifically, we get the recurrence relation Γ(z+1) = z Γ(z). Plotting the absolute value of the function in the complex plane yields the following surface, with poles situated at zero and the negative integers:
At certain non-integer arguments, we get new irrational constants. For example, Γ(1/2) is the square-root of π. Γ(1/4) is even more interesting, and has been shown (by Yuri Nesterenko, in 1996) to be algebraically independent of both π and e^π; in other words, there is no non-trivial polynomial in π, e^π and Γ(1/4) with integer coefficients that evaluates to zero.
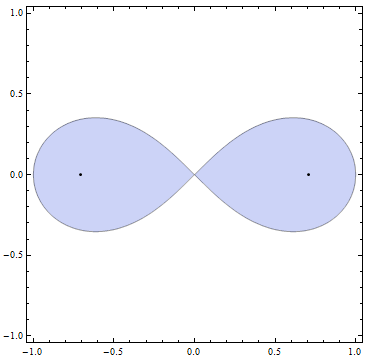
Also, we have , where S is the arc length of the lemniscate (shown above) given by the equation
(and, of course,
is our favourite transcendental constant). The area bounded by the curve is precisely 1, otherwise known as Legendre’s constant.
Related to this is Gauss’s constant:
AGM is the arithmetic-geometric mean, which is obtained by repeatedly iterating the map (x, y) → (√(xy), ½(x + y)) and taking the limit. There is an algorithm (the Brent-Salamin method) for calculating pi based on the arithmetic-geometric mean. The AGM converges extremely quickly, producing exponentially many digits of precision after n iterations. Nevertheless, the slower Chudnovsky algorithm is preferred for computing pi, due to the inefficiency of computing square roots.

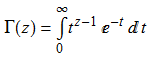
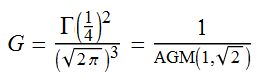
I always thought that complexity of multiplication, division, and square root is about the same… but then I realized there are ways of calculating multiplication which go below O(N^2) where N corresponds to precision.