I’m not sure exactly how to motivate a discussion of the Hoffman-Singleton graph, except perhaps by beginning with the following problem from the October 2011 edition of the Advanced Mentoring Scheme:
This problem seems quite innocuous at first, and one would not expect there to be particularly deep mathematics associated with it. Even more surprising is that there’s a very specific unsolved problem related to this.
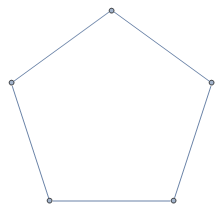
You might want to attempt this AMS question; it’s not particularly difficult. We can very quickly characterise these graphs as having diameter 2 (any pair of vertices can be connected by a path of length at most 2) and girth 5 (the length of the shortest cycle is 5), as well as noticing that every pair of vertices is contained in a 5-cycle, and so on. Pretty soon, it should be obvious that the smallest such graph is the pentagon itself:
Petersen graph
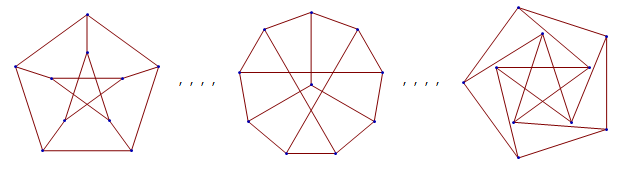
One may then wonder whether there are other graphs with this property. Generally, a good idea is to try your favourite graph. If you haven’t yet reached the stage where you have a favourite graph, adopt the Petersen graph as your newly-acquired favourite graph. Here are a few drawings of your favourite graph:
The leftmost diagram is the bog-standard drawing of the Petersen graph, which is the most instantly recognisable. The second one looks completely different, but more careful analysis demonstrates their equivalence. Taken together, it becomes clear that we’re dealing with a graph of immense symmetry. We can actually think of the Petersen graph as the skeleton of a dodecahedron, but with opposite vertices identified with each other. The complete graph K6 can be obtained by applying the same process to the icosahedron.
The third diagram differs only trivially from the first (there is a continuous deformation of the plane which relates them), and shows that the Petersen graph can be drawn such that all edges are the same length.
All of these drawings contain crossings, since the graph is non-planar (indeed, it is one of the simplest graphs that is not linklessly-embeddable) by virtue of having both the K5 and K3,3 as minors. It can, however, be drawn on the surface of a torus without crossings; I’ll leave the proof as an exercise to the reader.
Anyway, the point is that the Petersen graph satisfies the conditions specified in the problem.
Hoffman-Singleton graph
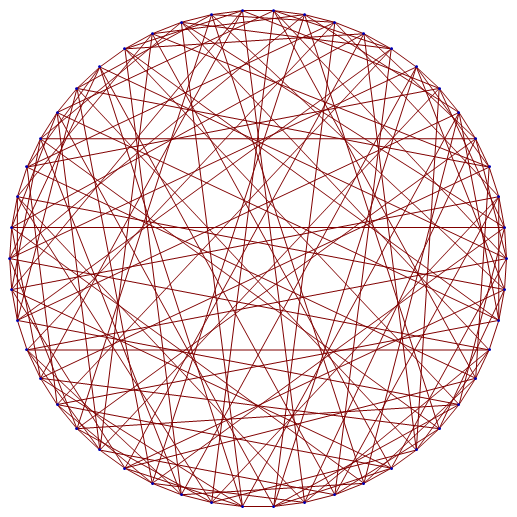
We’ve shown that there exist graphs of degree 2 and 3 with these properties. The next graph has degree 7, and is known as the Hoffman-Singleton graph. Noam Elkies proves its existence and uniqueness here.
Although it is not apparent from the rendering above, this graph is also massively symmetric. Ed Pegg provides a very elegant construction of the graph, which I’ll repeat below.
- Consider the 35 3-subsets of {1, 2, 3, 4, 5, 6, 7}. We’ll call these triads.
- Label the vertices of a Fano plane with the numbers {1, 2, 3, 4, 5, 6, 7}. By applying even permutations to the labels, we can obtain a total of
distinct labellings of the Fano plane. Ed refers to these as fanos.
- Let the 50 vertices of the Hoffman-Singleton graph be associated with the 35 triads and 15 fanos. We connect two triads with an edge if they are disjoint; we connect a triad to a fano if the former appears as a line in the latter.
It should be evident, with a little thought, that this gives a 7-regular graph. In fact, Pegg’s construction makes it straightforward to show that the conditions of the AMS problem are satisfied:
- Property (i) is obvious from the fact that it’s 7-regular.
- Property (ii) can be verified by a very short case check. No two fanos are connected, so three acquaintances must either (a) all be triads, or (b) one fano and two triads. Case (a) is impossible, since we cannot find three disjoint subsets of size 3 in the 7-element set {1,2,3,4,5,6,7}. Case (b) is similarly impossible, as we can’t find two disjoint lines in the Fano plane.
- Property (iii) takes slightly longer to verify. We split this into four cases, namely two fanos (c), one fano and unconnected triad (d), two triads intersecting in a single point (e) and two triads intersecting in two points (f). For case (c), note that two distinct fanos cannot share two lines (lest they are identical), so can share at most one. It’s similarly impossible for two fanos to have no common lines, so they must share precisely one. The corresponding triad, and only that triad, is connected to both fanos. For case (d), the three non-collinear points in the Fano plane can be extended to a set of four non-collinear points (an oval), the complement of which is a line disjoint from the original triad. In case (e), we can trivially embed the lines in a single labelled Fano plane. Case (f) is even easier: take the complement of the union of the two triads; this gives a third triad disjoint from the other two.
Hence, we can confirm that the Hoffman-Singleton graph actually works. Hooray!
Ed Pegg actually went further than merely constructing the graph; he designed a playable card game based on it. The case-bash above is precisely the solution to Pegg’s Puzzle E, showing that any two non-connected vertices have a unique common neighbour.
Although Pegg’s construction separates the vertices into clusters of sizes 15 (the fanos) and 35 (the triads), rest assured that the graph is actually vertex-transitive and thus all vertices are equivalent.
Beyond this?
It is a theorem, the Hoffman-Singleton theorem, that any graph satisfying those three properties must have either degree 2, 3, 7 or 57. In the first three cases, existence and uniqueness have been confirmed (with the pentagon, Petersen graph and Hoffman-Singleton graph, respectively).
As for degree 57, it is unknown whether such a graph exists. I very much hope that there is a unique such graph (since it would be another exceptional object, and exceptional objects are beautiful things), and there’s probably a really clever construction. It would have 3250 vertices and 92625 edges.
Observe that the Hoffman-Singleton graph contains lots of Petersen graphs, which in turn contain lots of pentagons. Similarly, I imagine that a degree-57 Moore graph would feature a plethora of Hoffman-Singleton graphs embedded within it.


Graphs can be more or less interesting. Let me say that if induced subgraph of a graph is interesting, then latter graph is at least that much interesting. Then, up to isomorphism, there exists most interesting graph – Rado graph! I think this is my favourite graph.
You’re arbitrarily asserting that a graph can have up to and including aleph-null vertices, and no more?
Sorry, while writing message I wanted to write “most interesting countable graph” but I forgot one word. Many uncountable graphs are interesting, like Aronszajn tree, or unit-length graph of real plane
Hmm, yes, the unit-distance graph of R^2 is interesting, precisely because its chromatic number is (by definition) the chromatic number of the plane. In that case, we only really care about its finite subgraphs, and it’s possible to find a countable graph with precisely the same set of finite subgraphs. (Proof: we can create a countable theory in first-order logic, with a statement for each finite graph, and say whether or not the graph occurs as a subgraph. Since an uncountable model exists (the real plane, R^2), so too must a countable model by Löwenheim-Skolem.)
Oh, I forgot to mention that Aronszajn trees are set-theoretic trees (partially-ordered sets), which can’t really be thought of as graphs (they don’t really have edges, nor can we impose a sensible edge set upon them).
“if induced subgraph of a graph is interesting, then latter graph is at least that much interesting”
This assumption is wrong. Counterexample: Take the Peterson Graph, add one vertex, and connect it to one other vertex. Now, some symmetries and lots of other interesting properties are destroyed, without any gain. So the new graph is less interesting, despite having the Peterson Graph as subgraph (and thus as induced subgraph).
Small correction: The last part
“… despite having the Peterson Graph as subgraph (and thus as induced subgraph).”
was meant to read:
“… despite having the Peterson Graph as subgraph – even as induced subgraph.”
Agreed.
I’m aware of this. But I hope you won’t deny Rado graph isn’t interesting. Maybe not most interesting, but not many infinite graphs have their own names 🙂
Yes, the Rado graph is interesting, but I agree with Volker that your assertion that a graph is at least as interesting as its induced subgraphs is false.
Pingback: The Not-Very-Random-At-All Graph | Complex Projective 4-Space
Pingback: Ten things you (possibly) didn’t know about the Petersen graph | Complex Projective 4-Space
Pingback: Leech lattice | Complex Projective 4-Space
Hello: how do you draw these pictures used in your blog? Were they created by Matlab or Mathematica?
Yes, I use Mathematica for the vast majority of the illustrations and diagrams.