A graph is vertex-transitive if its group of automorphisms acts transitively on the set of vertices. For example, the skeletons of uniform polyhedral are all vertex-transitive, as is the complete graph Kn. It’s obvious that a vertex-transitive graph must be regular, i.e. all vertices have the same degree.
Do all connected vertex-transitive graphs have a Hamiltonian cycle? Obviously not, since the second most basic connected vertex-transitive graph lacks one:
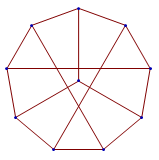
Is this the only counter-example? There are certainly no other obvious examples. In situations such as this one, it’s generally a good idea to employ the usual strategy of trying the Petersen graph. It does have a self-avoiding cycle of length 9, as shown in the embedding below, but not of length 10.
It transpires that only five counter-examples are known. In addition to K2 and the Petersen graph is the Coxeter graph, and graphs obtained by replacing each vertex of the Petersen and Coxeter graphs with triangles.
It is conjectured that these are the only counter-examples. Note that none of these are Cayley graphs (graphs whose vertices correspond to elements of a group, and edges correspond to multiplication by generators); indeed, the Petersen graph is the smallest vertex-transitive graph that is not a Cayley graph. Since all Cayley graphs are vertex-transitive, we obtain the following weaker conjecture:
Every Cayley graph contains a Hamiltonian cycle.
Consider the Cayley graph of the Rubik’s cube group, equipped with the twelve generators {U,U’,D,D’,L,L’,R,R’,F,F’,B,B’}. This has a vertex for each position of the Rubik’s cube, and an edge connecting two vertices if they differ by a quarter-turn. The existence of a Hamiltonian cycle is equivalent to the existence of a sequence of moves that visits every configuration exactly once before returning to the initial state.
A sequence of moves which eventually solves the Rubik’s cube irrespective of initial configuration is called a Devil’s algorithm. The Lovász conjecture, if true, would imply the following generalisation:
Every mechanical puzzle, the possible positions of which differ only in re-colouring the pieces, admits a Devil’s algorithm of length equal to the number of positions.
Indeed, this is actually equivalent to the Lovász conjecture on Cayley graphs, since every group can be expressed as the symmetries of some polytope in 