Clark Kimberling’s Encyclopedia of Triangle Centres contains several thousand triangle centres, many of which are defined as intersections of three concurrent lines. For example, we have:
- The three medians of a triangle intersect at the centroid;
- The three altitudes of a triangle intersect at the orthocentre;
- The three angle bisectors of a triangle intersect at the incentre;
- The three perpendicular bisectors intersect at the circumcentre.
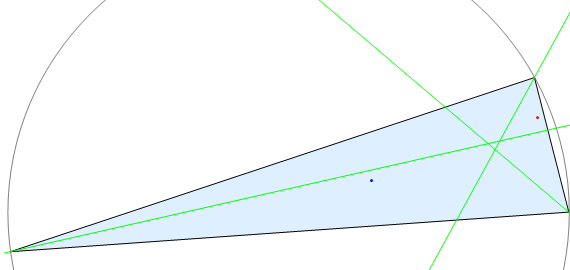
Indeed, it was joked that any symmetrically defined lines concur, the result being proclaimed the `symmetric geometry theorem’. Unfortunately, this is actually false, as shown by James Aaronson’s example of `the angular bisector of the median and the altitude’:
Hence, we don’t get a new triangle centre in this way.
Actual theorems
Nevertheless, there are many geometrical theorems with a large amount of symmetry, which we’ll refer to as `symmetric geometry theorems’. For instance, the configuration of Desargues’ theorem has 240 symmetries (isomorphic to S5 × C2) if you include projective duality. Similarly, Miquel’s six-circle theorem has 48 symmetries, which is evident by having the incidence structure of a cube:

Conway’s Petersen graph theorem
What was most interesting, however, was the following excerpt from an e-mail by John Conway, dated October 2003:
1. If two [sic] each vertex of the Petersen graph one assigns a line in 3-space, in such a way that all but one of the edges correspond to pairs of lines that intersect at right angles, then so does the last edge.
This seems quite remarkable. Ten lines give 40 real variables, and there are 28 linear constraints; this corresponds to 12 degrees of freedom. Also, note that if we replace ‘intersect at right angles’ with just ‘have perpendicular directions’, then the theorem must also hold: we can reduce it to the original situation by translating all lines so that they pass through the origin.
I tried to construct an example with lots of symmetry. A solution to the problem automatically induces a solution where the lines pass through the origin, so my first thought was to try the ten diameters passing through opposite vertices of a dodecahedron. Remarkably, this does have a Petersen graph incidence structure, but only when ‘at right angles’ is replaced with ‘at some other angle that I can’t be bothered to calculate’. Unfortunately, it doesn’t satisfy the original theorem, so any actual solution must have significantly lower symmetry than the Petersen graph itself.
Anyway, I found a single reference to this on a Math Overflow question, also from John Conway:
An equivalent version is the following: suppose you have a “right-angled hexagon” in 3-space, that is, six lines that cyclically meet at right angles. Suppose that they are otherwise in fairly generic position, e.g., opposite edges of the hexagon are skew lines. Then take these three pairs of opposite edges and draw their common perpendiculars (this is unique for skew lines). These three lines have a common perpendicular themselves.
The other examples on the page are purely projective theorems. Pappus’ theorem, Desargues’ theorem and Penrose’s ‘conic cube’ theorem are all self-dual, by the way. Here’s one of mine that isn’t self-dual, derivable from the quartic version of Cayley-Bacharach:
- Graph: rhombic dodecahedron;
- Vertices: six vertices are conics; the other eight are pairs of points;
- Edges: incidence;
- Statement: if five of the conics are present, then so is the remaining one.
It’s a grand generalisation of Miquel’s six circle theorem, with conics instead of circles and pairs of points instead of individual points.