This article can be regarded as a sequel to my 5 × 5 monotile. Since its announcement, several variants have been discovered. In particular, towards the end of this article we shall present a three-dimensional monotile with the following properties:
- Nonperiodic by the definition given in Socolar-Taylor (2010);
- No tiling has translational symmetry.
These properties have been independently achieved before (the first by the three-dimensional Socolar-Taylor tile; the second by the Schmitt-Conway-Danzer biprism and the aforementioned 5 × 5 monotile), but this appears to be the first time that a single prototile satisfies both properties. Unfortunately, the tiling still admits screw symmetry, so it is not strongly aperiodic.
Primitive and balanced monotiles
Note that the 5 × 5 monotile is completely specified by the pair (3 + 4i, 5) of Gaussian integers of equal norm. The first of these gives the period of the tile with respect to the grid of knobbles on the upper surface, and the second gives the period of the tile with respect to the grid of indentations on the lower surface.
A variant is described as primitive if (z, w) have equal norm and are coprime. The aforementioned example is not primitive, since we can take out a common factor of 1 + 2i, giving the primitive pair (1 + 2i, 1 − 2i). Since the periods are complex conjugates, we describe the monotile as being balanced.
Note that, unlike the examples where w is an integer, we’re not actually allowed to have the knobbles protruding over the edge, since that would result in the indentations also protruding (obviously impossible).
If a balanced tile is flipped over, the knobbles and indentations precisely switch positions. If, instead, we replace both the knobbles and indentations with a self-complementary shape, then the tile will have dihedral symmetry (invariant under being flipped over). This will be useful for the culmination of this article: a nonperiodic translation-free monotile.
Hexagonal variants
Warren Smith (of n-body fame) proposed a hexagonal variant, based upon the Eisenstein integers rather than the Gaussian integers. The simplest primitive balanced monotile has seven knobbles and is specified by the pair (3 + ω, 3 − ω), where ω is a primitive cube root of unity.
As described at the end of the previous section, this can be modified to give a self-complementary variant invariant under the operation of ‘flipping over’, and exhibiting a rotational symmetry group isomorphic to the dihedral group D12. (For an explicit construction, replace each knobble and indentation with a hexagonally-symmetric ring of alternating pegs and grooves.)
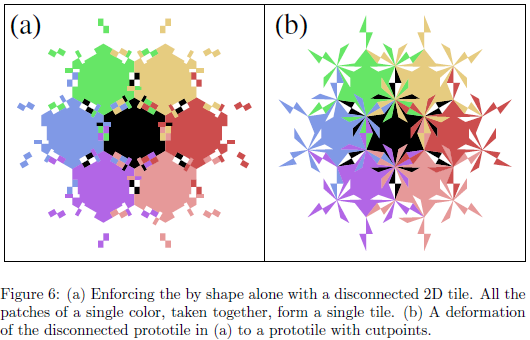
So far, this is no qualitatively different from the monotiles discussed earlier. However, we can then slice this hexagonal prism along its equator, separating the two halves slightly and inserting [the Cartesian product of an interval with] a Taylor-Socolar aperiodic monotile. In particular, we choose the disconnected variant from Figure 6 of the paper by Socolar and Taylor:
The problem with this is that we now have a disconnected 3D tile with the desired properties (nonperiodic and translation-free). Nevertheless, it can be converted into a connected tile (indeed, a polyhedron) by ‘skewering’ the other connected components with helical protrusions, and boring complementary helical holes in the prisms (c.f. duck genitalia, but without the problematic chirality issues).