Given a real number x, computing its continued fraction can reveal a lot of information. In the simplest case, the continued fraction terminates if and only if the number is rational. One particular example of this is the rational , the continued fraction of which is shown below:
(The square-bracketed expression [3; 7, 16] is just a convenient notation for the continued fraction expansion.)
Rational numbers are simply the roots of linear polynomials with integer coefficients. Hence, the next simplest case is when x is the root of a quadratic equation with integer coefficients. It transpires that this is equivalent to the continued fraction being eventually periodic, such as , where the sequence (2, 1, 3, 1, 2, 8) is repeated indefinitely.
Roots of higher-degree irreducible polynomials, along with transcendental numbers, all have aperiodic continued fractions. Some of these are simple and predictable, such as , whereas others seem to exhibit no obvious patterns, such as π. However, this article is concerned with algebraic numbers rather than transcendental ones, so the next cases to explore are roots of cubics.
Brillhart’s cubic
In 1965, Brillhart noticed that the positive real root of the depressed cubic x³ − 8x − 10 has an ‘exotic’ continued fraction. This algebraic number is equivalently the dominant eigenvalue of the following 3 × 3 matrix:
What makes the continued fraction exotic is the presence of large terms early in the expansion:
[3; 3, 7, 4, 2, 30, 1, 8, 3, 1, 1, 1, 9, 2, 2, 1, 3, 22986, 2, 1, 32, 8, 2, 1, 8, 55, 1, 5, 2, 28, 1, 5, 1, 1501790, 1, 2, 1, 7, 6, 1, 1, 5, 2, 1, 6, 2, 2, 1, 2, 1, 1, 3, 1, 3, 1, 2, 4, 3, 1, 35657, 1, 17, 2, 15, 1, 1, 2, 1, 1, 5, 3, 2, 1, 1, 7, 2, 1, 7, 1, 3, 25, 49405, 1, 1, 3, 1, 1, 4, 1, 2, 15, 1, 2, 83, 1, 162, 2, 1, 1, 1, 2, 2, 1, 53460, 1, 6, 4, 3, 4, 13, 5, 15, 6, 1, 4, 1, 4, 1, 1, 2, 1, 16467250, 1, 3, 1, 7, 2, 6, 1, 95, 20, 1, 2, 1, 6, 1, 1, 8, 1, 48120, 1, 2, 17, 2, 1, 2, 1, 4, 2, 3, 1, 2, 23, 3, 2, 1, 1, 1, 2, 1, 27, 325927, 1, 60, 1, 87, 1, 2, 1, 5, 1, 1, 1, 2, 2, 2, 2, 2, 17, 4, 9, 9, 1, 7, 11, 1, 2, 9, 1, 14, 4, 6, 1, 22, 11, 1, 1, 1, 1, 4, 1, 3, 2, 1, 2, 1, 1, 2, 4, 2, 1, 5, 1, 8, 2, 2, 5, 1, 2, 1, 1, 1, 1, 1, 3, …]
To understand why that occurs, it helps to have an exact closed form for the root. Fortunately, that’s not too hard, since we know how to solve a depressed cubic. In particular, we equate x³ − 8x − 10 with the ‘difference of three cubes’ x³ + a³ + b³ − 3abx. Equating coefficients, we get:
- a³ + b³ = −10
- ab = 8/3
We can easily solve the resulting quadratic equation to obtain a and b. Then, the real root is simply x = −(a + b), which is given by:
Note that the is significant, as 163 is a Heegner number (the ring of integers in the quadratic field
is a unique factorisation domain). The reason for the large partial quotients in the continued fraction expansion was explained by Stark, who incidentally was the first person to correctly prove Gauss’s conjecture that the Heegner numbers are precisely {1, 2, 3, 7, 11, 19, 43, 67, 163}.

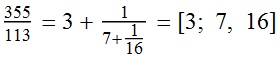
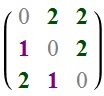
This post could do with more references / links. “Brillhart noticed” – reference / link to where he did so? “was explained by Stark” – reference / link? (Actually, it could do with saying something more about the explanation; it’s a bit disappointing just to lead up to “was explained by” rather than an actual explanation. Even if “was explained by” linked to a paper by Stark as it should, that paper may not be the best level of explanation for casual blog readers.) I think I’ve mentioned to you before that generally when you refer to some piece of known mathematics – theorem, mathematical object, announcement of new result, etc. – you should routinely give a reference or link (to the original paper or announcement, where appropriate).
Stark’s paper is `An explanation of some exotic continued fractions found by Brillhart’, but it doesn’t appear to be on the Internet.
I knew Heegner numbers have many interesting and odd properties, but I didn’t know about this one. Are we guaranteed that such peeks will appear later on, or may expansion at some point become more stabilized?
I think that it plateaus off, and asymptotically obeys Khintchine’s law.
According to Bombieri & Poorten (http://maths.mq.edu.au/~alf/www-centre/alfpapers/a113.pdf) the final exotic partial quotient is c161 = 325927.
After that the series “settles down to normalacy”.
レディース 財布 rolex デイトナ http://fangshena.gagajpdoninfinite.org/