Perrin sequence

The Perrin sequence is defined by a recurrence relation, and is qualitatively similar to the Lucas sequence. The initial terms are and subsequent terms are defined by , and summarised in the following spiral of equilateral triangles:

As you can see, I’ve cheated slightly by tucking a corner of beneath . This is because the spiral was designed for the Padovan sequence, which is to the Perrin sequence as the Fibonacci sequence is to the Lucas sequence. This analogy can be made precise by considering the closed form of the Perrin sequence:

These Greek letters are the roots of the characteristic polynomial x³ − x − 1 = 0. They can be computed by an easy application of Tartaglia’s method for solving the cubic, but the resulting expression is messy and not particularly insightful. The closed form, however, can be used to deduce that if p is prime, then p divides P(p):

modulo p.

The non-trivial step can be deduced by expanding the expression , which gives p multiplied by some symmetric polynomial (as all non-trivial multinomial coefficients are divisible by p), which in turn can be expressed as a polynomial in the elementary symmetric polynomials (thanks to Newton’s theorem), which are all integers (by Vieta’s formulae). This result is a massive generalisation of the freshman’s dream.

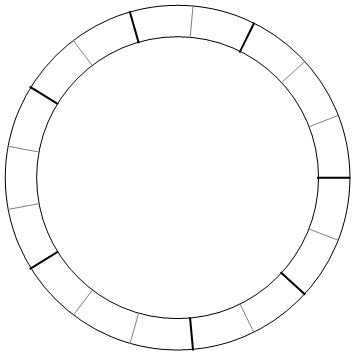
A nicer way to prove that p divides P(p) is by noticing that P(p) counts the number of ways to tile an order-p cycle graph with tiles of length 2 or 3 (or, equivalently, the number of maximal independent sets). Here is an example tiling for p = 17:

When acted upon by the cyclic group Cp of rotations, no tiling can have a non-trivial stabiliser. Hence, the tilings are partitioned into orbits of size p, so the total number of tilings must be divisible by p. This argument generalises to any depressed monic polynomial with integer coefficients, as does the proof involving multinomial coefficients.

This can be exploited to give a Fermat-style test for primality. If n does not divide P(n), then n must be composite. We can compute this residue in O(log² n log log n log log log n) by using a matrix form of the recurrence relation, repeated squaring and the Schönhage-Strassen algorithm for multiplication.

Perrin pseudoprimes appear to be rarer than Fermat pseudoprimes, with only 17 below 10^9 compared with 646 Carmichael numbers and 5597 base-2 pseudoprimes in this interval. The smallest is 521² = 271441, followed by 904631 and 16532714. It’s possible to make better primality tests by (for instance) combining the Perrin, Lucas and Fermat primality tests. I don’t know of any composite numbers that are simultaneously Perrin and Lucas pseudoprimes, but they most probably exist.