In the not-too-distant future, people are going to be celebrating the 100th birthday of Bill Tutte. He’s not quite as well-known as Alan Turing, which is a shame since they were both equally invaluable in the cryptanalysis at Bletchley Park. You may also know him from the problem of squaring the square, which he accomplished with three of his friends whilst they were students at Trinity. The story of how they met was rather interesting and extremely serendipitous, and is recounted at the beginning of this article on squaring.net.
The catalysis for this was a complete chance encounter in London between Trinity mathmos Arthur Stone and Cedric Smith, who happened to both reside in the area. The scope of the conversation was as vacuous as the empty set, and not even their names were exchanged at the time. Much more interesting was the next edge of the acquaintance graph, which was created in an equally improbable manner:
As first-year undergraduates, Cedric Smith met Rowland Brooks in a lecture on almost periodic functions. This was the equivalent of a Part III lecture, and their attendance was the result of an error in a timetable. This administrative mistake became apparent from the incomprehensibility of the lecture! Nevertheless, it was very fortunate that the timetables were erroneous, since it ultimately led to a very productive union of four mathematicians.
The fourth, of course, was Bill Tutte, who was reading chemistry (which has since been engulfed into the Natural Sciences Tripos) as well as mathematics. He knew Rowland Brooks, and later met Smith and Stone by extension. Tutte will be the primary focus of the majority of this article, so it seems appropriate to include a picture. Even better, here is a photograph of a bronze bust by the accomplished sculptor, artist, painter and former musician, singer and actress, Gabriella Bollobás, who happens to be married to the eminent mathematician Professor Bollobás:
Squaring the square
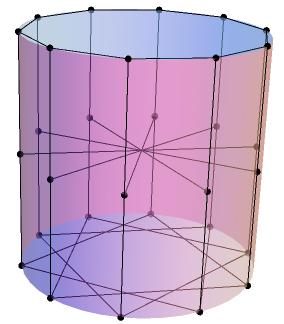
The four of them met on a regular basis to discuss mathematical problems. One of these was the problem of finding a squared square, that is to say a dissection of a square into a finite number of smaller squares, no two of which are the same size. William Tutte wrote a detailed account of their effort to solve this mathematical problem, which spanned the years 1936 through to 1938.
The first major insight was that a squared rectangle could be represented by a network of one-ohm resistors, where the Thevenin equivalent resistance is equal to the aspect ratio of the squared rectangle. Specifically, imagine that the rectangle is made from a material of uniform resistivity, where a square of the material has a resistance of one ohm between opposite edges. Then, given a dissection of the rectangle into squares, we can replace each horizontal line with a perfect conductor, and each vertical line with a perfect insulator, and since all current flows vertically this has no effect on the total resistance.
A corollary of this is that the resulting squared rectangle must have sides in a ratio corresponding to the resistance of a circuit composed of one-ohm resistors; this forces it to be rational. Tutte et al also showed that the dimensions of the constituent squares must also be commensurate with the side lengths of the rectangle.
The next important discovery was by Smith’s mother, who assembled the squares into a perfect rectangle in a different arrangement from the original configuration. Eventually, it was noticed that this corresponded to a resistance-preserving transformation of the corresponding electrical circuit. They reasoned that it might be possible to tile the same rectangle with two completely different sets of squares, which would trivially result in a squared square:

Problematically, the squared rectangle produced by Smith’s mother featured precisely the same set of squares as the original, so the resulting dissection of the square would be replete with pairs of identical squares. Hence, further ingenuity was required to discover a perfect squared square.
The structure of Smith’s circuit was observed to naturally partition into a ‘rotor’ with threefold rotational symmetry and a ‘stator’. With a one-wire stator, it was realised that it could be possible to produce two rectangles sharing only one common square, which could be overlapped to yield a configuration trivially completable into a squared square. It transpires that Smith and Stone collaboratively found one, at almost precisely the same time that Brooks did so.
These order-69 squares were the first to be discovered, but far from being optimal. The Trinity Mathematical Society logo is an order-21 squared square, which has been proved to be minimal by exhaustive search.
Cryptanalysis of the Lorenz cipher
A year later, Britain and Germany plunged into the Second World War. (I’m not going to mention the war again, I promise!) This involved quite a lot of secret communication on both sides, and much of the Allied codebreaking efforts were concentrated in Bletchley Park.
Bletchley Park defeated two great ciphers. The first of these, which is probably more well known, was Arthur Scherbius’ Enigma cipher used by the Luftwaffe and Kriegsmarine. The effort began with the Polish mathematician Marian Rejewski. He knew roughly how the Enigma worked from models stolen by intelligence agencies, but had to embrace the immense challenge of determining both the internal wiring of the rotors and a method for cryptanalysing the variable key (which changes with each day). Rejewski built a machine, the bomba, for brute-forcing the key settings. Eventually, the Polish intelligence passed their discoveries to Bletchley Park, where people such as Alan Turing (King’s College, Cambridge) and Gordon Welchman (Trinity, yet again) found alternative and more flexible methods of cryptanalysing the Enigma based on Rejewski’s insights.
However, the cryptanalysis of the more difficult Lorenz cipher was an infinitely more impressive achievement, mainly because it was accomplished without anyone having ever seen one of the Lorenz encryption machines. I shall briefly describe its modus operandi.

The Lorenz cipher used the Baudot code, where each character is represented by five binary digits (either dots or crosses). The enciphering machine (or Schlüsselzusatz) produced a pseudorandom stream of information which was XOR’d with the plaintext to yield a ciphertext. The same stream of information, when XOR’d with the incoming ciphertext, would result in perfectly comprehensible plaintext. This Vernam cipher was a known form of encryption, but cryptanalysists at Bletchley Park had no idea how the pseudorandom bit generator operated.
What would be helpful is if the output of the pseudorandom bit generator could actually be isolated. This happened when a lazy operator was asked to repeat a message with the same key, and abbreviated it slightly, giving a huge vulnerability. Specifically, XORing the two encrypted messages would neutralise the contribution of the Schlüsselzusatz, giving the symmetric difference of the two messages. John Tiltman was able to carefully separate this into the two original messages, treating it as a basic autokey cipher. Moreover, he could XOR the encrypted and decrypted messages to isolate the output of the Schlüsselzusatz.
Enter Tutte. Tutte was given the output of the Schlüsselzusatz, and asked to deduce the internal workings of the machine. This, of course, was an incredibly difficult task. He started by looking for approximate periodicity (perhaps the lecture on almost periodic functions helped!) in the bitstream. He found a period-41 pattern, suggesting the presence of a rotor χ1 with 41 teeth. Moreover, he determined that another more complicated rotor (ψ1) driven by a motor wheel μ contributed to the encryption. Proceeding in this manner, cryptanalysts determined how each of the other four bits were generated (there were five independent mechanisms with coprime periods).
Armed with Tutte’s deduction, Alan Turing et al were able to work on algorithmically cracking this cipher. This began with the electromechanical Heath Robinson machines, which were replaced by the much more efficient electronic Colossus computers, designed and built by engineer Tommy Flowers. Gordon Welchman was somewhat disapproving of this shift from good old electromechanical relays to those new-fangled thermionic valves; fortunately, Turing was more forgiving. Nowadays, of course, relays and valves have both been rendered obsolete by microscopic transistors on silicon chips, and may eventually be further antiquated by advances in carbon nanotechnology.
The intercepted and decrypted communications gave the Allies a massive advantage. I seem to recall that they even sent a Lorenz-encrypted message to sabotage the Nazi military by issuing unhelpful orders, although I might be confusing this with the Sherlock Holmes mystery, The Adventure of the Dancing Men.
![]()
Graph theory
Squaring the square, whilst initially appearing to be combinatorial geometry, eventually succumbed to a graph-theoretic approach. Many of Bill Tutte’s mathematical accomplishments were in graph theory, including the disproof of Tait’s conjecture that every 3-regular polyhedral graph admits a Hamiltonian cycle.
He has a few graphs named after him, one of which is the Tutte 8-cage. This is a 3-regular graph with girth 8, and indeed is the unique smallest such graph. It possesses a large amount of symmetry, a small amount of which is apparent in the following picture:
Its full symmetry group is PΛL(2,9), the automorphism group of S6. This is apparent from the standard construction of the 8-cage: take the 15 unordered pairs of letters {a,b,c,d,e,f}, together with the 15 unordered triples of unordered pairs (such as (ac,bf,de)), and connect a triple to a pair when they are incident. This has an obvious action of S6 (permuting the letters), but also features an outer automorphism interchanging the two halves of this bipartite graph. Indeed, this is one of the simplest ways to see the outer automorphism of S6.
Tutte was also responsible for the snark conjecture, that every snark contains the Petersen graph as a minor. When proved much later by Robertson, Seymour et al, this gave an indirect proof of the four colour theorem as an immediate corollary. Other theorems include the BEST theorem (where the ‘T’ in the acronym stands for ‘Tutte’), Tutte-Berge formula and Tutte’s homotopy theorem.
William Tutte passed away in 2002, after a long life (by contrast with Turing’s untimely cyanide-laced Rosacaean death) and a very fruitful and productive mathematical career. There is an obituary in the Guardian.


Pingback: Descartes snark | Complex Projective 4-Space
My names is Alison Hayes and I am chairman of the Bill Tutte Memorial Working group based in Newmarket, in Suffolk, UK, the town where Bill was born. For the past two years we have been raising funds for a commemorative sculpture called The Codebreaker, which is will be unveiled this September to mark Bill’s wartime codebreaking achievements, which as you recognised, do not get anything like as much recognition as those of Alan Turing. Go to http://www.billtuttememorial.org.uk to see more. We are also collected funds for a Bill Tutte scholarship under which we plan to award a grant of £1000 per year for three years to a local student going to study maths and/or computer science at university. Could you tell me where the bust featured in your article is ? Someone told me it was in the Microsoft headquarters ?
Best regards
Alison
Hello, Alison.
This is excellent news, thank you; I am very pleased that Tutte’s revolutionary work will be adequately commemorated. The punched-tape panels are brilliant, and I may even visit the sculpture when it is unveiled (to coincide with the centenary?). I approve of the scholarship as well — is it specific to Trinity College, Cambridge (where Tutte matriculated), or applicable to any university?
I’m not sure where the bust is located, but I’ll ask Gabriella Bollobás directly (serendipitously, she has e-mailed me to confirm my booking of a seat at a performance of Schubert’s Winterreise, so I’ll enquire when I reply to the e-mail) and notify you accordingly.
Sincerely,
Adam P. Goucher
I spoke to Gabriella at the Winterreise. Apparently, she is going to be sculpting another W. T. Tutte bust.
Thanks for your job.
A greeting.