The Tammes problem asks for an arrangement of n points on the surface of a sphere, which maximises the minimum distance between any two points. This can be regarded as the classic problem of circle packing, but on the sphere (endowed with the usual metric) instead of a bounded region of the plane.
For n = 1, the problem is completely trivial. It should be easy to convince yourself that for 2, 3 or 4 points, they are placed at the vertices of a regular (n − 1)-simplex with unit circumradius; the last case corresponds to a regular tetrahedron. For n = 6, the best arrangement is the octahedral one. Solutions to Tammes’ problem roughly correspond to molecular configurations, although the molecular energy-minimisation problem is not quite the same as the minimax problem.
For n = 8, 12 and 24, the optimal solutions are the square antiprism (not the cube!), icosahedron and snub cube, respectively. The metric properties of the uniform snub cube involve the tribonacci constant (limiting ratio of successive terms of any non-trivial sequence such that each term is the sum of the three preceding terms), in a similar way to how the dodecahedron and icosahedron involve the golden ratio.
Anyway, you may notice that I’ve postponed discussion of the case n = 5. It transpires that we can’t arrange five points with a minimum angle greater than 90°, and with that minimum angle, it is always possible to add a sixth point (to give the octahedral vertex arrangement). It transpires that in chemistry, the favourable structure is a trigonal bipyramid (the north and south poles, together with three equidistant equatorial points).
Now, suppose we had a molecule with five distinguishable functional groups connected to a single atom in this arrangement. There are obviously 120 permutations of the functional groups, but these can be partitioned into twenty sets of six under the equivalence relation ‘rotations are equivalent’. Hence, there are precisely twenty isomers.
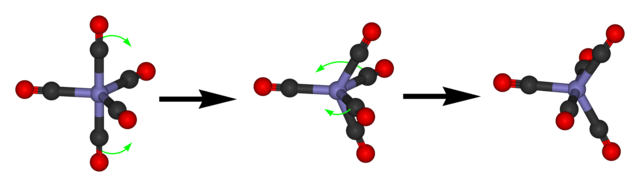
The Berry mechanism (shown above) gives a method to convert one isomer into another. The obvious thing to do at this point is to draw a graph, with a vertex for each isomer and an edge for each application of the Berry mechanism. We can immediately deduce that it is 3-regular and has 20 vertices. Also, note that rotations correspond to even permutations of the functional groups, wheread applications of the Berry mechanism correspond to odd permutations; hence, the graph is bipartite. Finally, if we partition the isomers into ten pairs of enantiomers, we can label each pair by the two axial (non-equatorial) functional groups, and note that the Berry mechanism must always change both axial groups.
Consequently, by the definition of the Petersen graph as a Kneser graph, we can deduce that this 20-vertex configuration must be the bipartite double cover of the Petersen graph, namely the Desargues graph. Organic chemists refer to this as the Desargues-Levi graph.
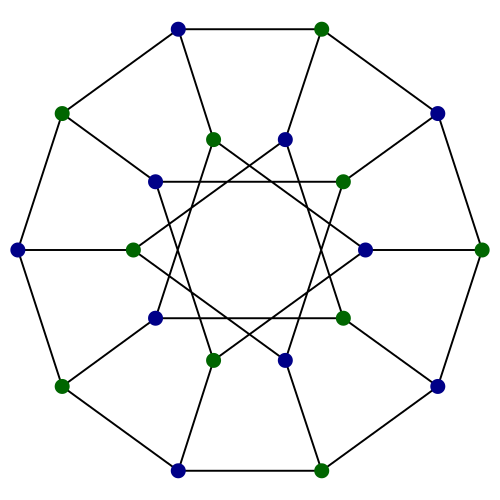
In a non-orientable universe such as a three-dimensional analogue of the Klein bottle, there are no such things as chiral compounds (enantiomers can be interchanged by rigid motions) and this graph would reduce to the Petersen graph. Indeed, the chemistry of a non-orientable universe would be very interesting. One can begin to speculate what would happen:
In the year 3000, an intrepid explorer embarks upon a voyage in a cutting-edge spaceship, endowed with the ability to travel at superluminal speeds. Upon leaving our Solar system, she overtakes the Voyager probes in an instant, passes through the Oort cloud in a few seconds, and continues in the general direction of the Andromeda galaxy. Increasing her speed yet further, the entire universe flashes past her, and she finds herself approaching a pleasantly wet planet.
She disembarks on an island, and finds a coniferous forest populated with pine trees. After convincing herself that it is safe to remove her oxygen mask, she is greeted by the smell of lemons. In spite of this, there are no lemon trees in sight. Proceeding slightly further, she notices a sign marked with strange symbols — evidence of intelligent life?
It transpires that travelling billions of lightyears is a rather exhausting experience, thus leaving our protagonist completely famished. Hence, it was serendipitous that she encountered a restaurant, and even more serendipitous that everyone there happened to speak English, despite having distinct writing. Delving into a three-course meal seemed to be a good idea at the time, and is rarely inadvisable. However, somewhere between the main course and the dessert, she passed away.
Basically, reflected food is at least incompatible with our digestive systems, and possibly even poisonous (Lewis Carroll suggested this in Alice Through The Looking Glass). As for the citric-scented pine trees, it is a consequence of the molecule limonene, the enantiomers of which have different aromas (D-limonene gives citrus fruits their distinctive smell, whereas L-limonene is found in pine needles).
Fortunately, our universe must be orientable due to a phenomenon called CP-violation, which essentially means that physics has chiral properties. Hence, the situation I envisaged above is theoretically impossible.
Chirality occurs in inorganic chemistry as well as organic chemistry, with several crystals lacking reflectional symmetry. Indeed, crystallographers count some three-dimensional crystallographic symmetry groups twice, as the left-handed and right-handed groups are not conjugate in the larger group of rigid motions. This behaviour does not have an analogue amongst any of the 17 two-dimensional wallpaper groups.
In fact, I forgot to mention that the Leech lattice is chiral, and can be characterised as the unique chiral even unimodular lattice of lowest dimension. Returning full circle, the arrangement of shortest vectors in the Leech lattice gives a unique optimal solution to Tammes’ problem in 24 dimensions.


So, what is the solution to the Tammes Problem for n=7? Does it work out the same way as the n=5 problem, in that the minimal angle is no greater than the minimal angle for 8 points? I looked it up on wikipedia, but the page was very short and didn’t give any further information on the problem.
I’ve researched a bit more, and I found out that this problem is related to the kissing number problem, if you modify the kissing problem to say: How big can you make N spheres but still have them all touch a unit sphere.
We can consider Tammes problem as problem of finding function f:N->(0,2pi) such that f(n) is angle being value in our minimax problem. I’ll be really surprised if this function had continuation to real domain, because f(5)=f(6)=pi/2, and other than that it seems strictly decreasing.