Consider the Riemann sphere, obtained by adjoining a ‘point at infinity’ to the complex plane. The conformal maps from the Riemann sphere to itself form a group, the Möbius group, which is abstractly isomorphic to (and also the proper orthochronous Lorentz group
, although I’ll discuss that later). Douglas Arnold and Jonathan Rogness made an excellent illustrative video:
[youtube=http://www.youtube.com/watch?v=JX3VmDgiFnY]
One way to construct the Möbius group is to embed it in a larger group generated by reflections in arbitrary lines and inversions in arbitrary circles, and to just take the index-2 subgroup of transformations that preserve orientation instead of reversing it. This is exactly analogous to the distinction between the orthogonal group and the special orthogonal group.
However, this larger group is interesting in its own right. But what should it be called? It can be thought of as ‘the group generated by Möbius transformations together with the field automorphism of complex conjugation’, and one would be very tempted to call this the projective semilinear group . So far, so good?
Actually, no.
Complex field automorphisms
In addition to complex conjugation, there are loads of silly field automorphisms of the complex numbers, obtainable by invoking the axiom of choice. Indeed, it’s a rather routine exercise:
- Well-order the complex numbers, bijecting them to the initial ordinal of the correct cardinality. (This is the first line of most proofs involving the well-ordering principle.)
- Cross out all of the algebraic numbers.
- Choose the first complex number that isn’t in your well-ordering, and dump it into a set called ‘the generators’.
- Cross out all of the numbers in the well-ordering that are not algebraically independent of ‘the generators’.
- Repeat steps 3 and 4 uncountably many times, until we’ve exhausted the ‘list’ of complex numbers. Don’t worry; even though this sounds illicit, it is permissible by transfinite induction.
Now, permutations of the generators give silly field automorphisms of the complex numbers. Hence, the projective semilinear group is not just the Möbius group with reflections, but instead a ridiculously large group that we don’t care about.
These pathological automorphisms actually lead to some pathological geometric transformations of the complex projective plane, as described in a fascinating paper. These transformations map lines to lines, circles to circles, conics to conics and so on, yet are spectacularly discontinuous.
Hyperbolic geometry and the Lorentz group
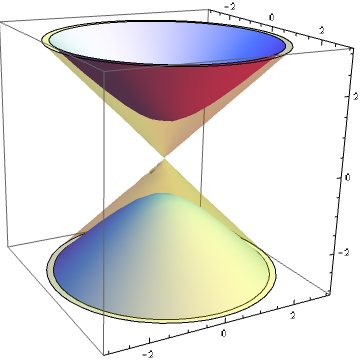
Consider spacetime with one temporal and two spatial dimensions. It looks something like this:
The Lorentz group consists, unsurprisingly, of the Lorentz transformations, which are the linear transformations preserving the Minkowski dot product. Equivalently, they are the linear transformations fixing that hyperboloid of two sheets. If we discard one of the sheets, we obtain the orthochronous (time-preserving) subgroup.
From the perspective of the centre of the cone, the hyperboloid looks like an open disc. The orthochronous Lorentz transformations precisely correspond to distance-preserving transformations of the hyperbolic plane. These are themselves determined uniquely by a conformal (or anticonformal) transformation of the ‘circle at infinity’.
Adding an extra dimension, the orthochronous Lorentz group is isomorphic to the group of distance-preserving transformations of hyperbolic 3-space, which is again isomorphic to the group of (anti-)conformal transformations of the ‘sphere at infinity’, namely our index-2 supergroup of the Möbius group.
Moreover, this nicely generalises: the group generated by geometric inversions on the n-sphere is abstractly isomorphic to the orthochronous Lorentz group . And when n = 24, we get a very beautiful discrete subgroup, namely the automorphism group of the II(25,1) lattice intimately related to the Leech lattice.

Here’s a real riddler: we have all kinds of math suggesting that 26-dimensional spacetime is something special. The above, the Moonshine conjecture, etc.
26-dimensional spacetime is predicted by one particular candidate ultimate theory of physics: non-supersymmetric string theory.
On the other hand, physicists have found that supersymmetry seems “too beautiful to be wrong”. And whereas the Standard Model and non-supersymmetric extensions to it permit a very broad range of possible Higgs masses, supersymmetry constrains it to be in a narrow range near 125 GeV, which is where it was just found.
So we have a kind of “strong mathematical circumstantial evidence” in favor of non-supersymmetric string theory, but strong particle-accelerator circumstantial evidence in favor of supersymmetry (else that Higgs mass just so happening to lie in the narrow range compatible with supersymmetry, despite not having to, is one heckuva weird coincidence).
I’d have to go with the physical evidence at this time and favor supersymmetry, which forces string theory to live in ten dimensions instead of 26 (so a 9+1 manifold instead of 25+1).
Yet it would be beautiful if the discrete subgroup related to the Leech lattice (which IIRC is a double cover of Co1, plus the PT symmetries of physics, plus translations — so that double cover would be the orientation-preseving, non-time-reversing point group, wouldn’t it?) turned out to be the key to unifying physics…
Supersymmetry also predicts a fermion for ever boson and vice-versa, none of which have been discovered. Hence, I’m not so sure that supersymmetry is favoured by physical evidence.
The automorphism group of II(25,1), once we restrict to orthochronous (non-time-preserving) transformations, has a reflection group whose Coxeter-Dynkin diagram has the structure of the Leech lattice, modulo which is the group of graph automorphisms, i.e. Co0 with translations.
II(25,1) is trivial to construct, and directly ‘explains’ the Leech lattice and 1² + … + 24² = 70². The Leech lattice in turn ‘explains’ many of the sporadic groups, in addition to the E8 lattice and the Golay code. II(25,1) can be used to construct the monster vertex algebra (and thus the monster group), but it’s non-trivial unlike the construction of the Leech lattice from II(25,1).
There are lattices II(8n+1,1) for each non-negative integer n, so we get nice Lorentzian lattices in 9+1 and 17+1 dimensions. The first of these corresponds to the tessellation obtained by continuing the sequence:
E6 polytope, E7 polytope, E8 polytope, E8 honeycomb, E9 hyperbolic honeycomb, ….
II(17,1) also has a finite Coxeter-Dynkin diagram with a graph automorphism group of 2. II(25,1) has an infinite Coxeter-Dynkin diagram, as I described (since the Weyl vector has a norm of 0), and the higher lattices have no analogue of the Weyl vector.
Hence, the II(25,1) lattice is really exceptional, more so than the II(9,1) living in ten-dimensional spacetime. I agree that it would be beautiful if our universe had this string theory, as it’s the same string theory used to construct the monster vertex algebra.
Does the group of all continuous maps from 2-sphere to itself have any special name? If not, how about maps on circle?
Do you mean homeomorphisms (continuous bijections with continuous inverses)? Continuous maps are in general non-invertible.
Anyway, the group of homeomorphisms is unimaginatively called the homeomorphism group:
https://en.wikipedia.org/wiki/Homeomorphism_group
Actually, I meant group of all continuous maps (not necessarily injections or bijections), but now I realised that for this to be group maps need to be bijective and bicontinuous.
On a related note, is there a simple example of continuous bijection from sphere to sphere without continuous inverse? I know example for disc with segment of boundary removed, but not for sphere nor circle.