It’s now New Year’s Eve, which is why the cp4space banner has changed again.
As is usual for this time of year, there is a joint Anglo-Hungarian IMO training camp in Tata, Hungary. I’ve mentioned it before at the end of 2012, but perhaps it is worth re-iterating that this is where Complex Projective 4-Space was originally popularised. I shall start by discussing a problem that appeared on the selection test at the end of this camp two years ago, which recently resurfaced on an online forum.
Given any arrangement of white and black tokens along the circumference of a circle, we’re allowed the following operations- take out a white token and change the colour of both its neighbours, or put in a white token and change the colour of both its neighbours. Is it possible to go from a configuration with just two tokens, both white, to a configuration with two tokens, both black?
You may want to attempt this problem for yourself before reading further. One of the members of the forum posted graphs of what appear to be three equivalence classes of ‘necklaces’ (we shall later prove whether or not this is actually the case), where edges represent elementary operations. Here is one of the equivalence classes:

I had seen an ‘official’ solution to this problem, but as is usual for official solutions, it was not particularly insightful. By contrast, Gabriel Gendler devised a much more interesting interpretation, which, whilst essentially equivalent to the official solution, offers far more insight and generalises beautifully.
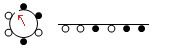
The idea is to ‘break’ the necklace at an arbitrary prespecified point, so that the beads form a linear string. For example, we can break the following necklace at the point specified by the arrow to give a linear string:
This string will be represented as WWBWBB. Cutting the same necklace at a different point would give a different string, such as WBWBBW, but we will consider this caveat later. For now, we will focus on the simpler problem where the string is linear, rather than cyclic. This is the famous word problem, which is undecidable in general but easy in this particular case. We can summarise the elementary operations as relations:
-
BWB = WW
- BWW = WB
- WWB = BW
- WWW = BB
If we allow the elements to have inverses, then this becomes a group presentation. Gabriel noticed that in particular, this is a presentation for the permutation group S3, where B = (1 2) is a transposition and W = (1 2 3) is a 3-cycle. We can convert between words only if* they represent the same group element in S3.
* Again, if we allow inverses, things become much neater and the converse also holds. Otherwise, it is necessary to consider small cases separately.
However, we now need to remember that in the original problem, the string is cyclic. Hence, where x and y are arbitrary strings, xy and yx represent the same necklace cut at different places. Consequently, as well as the local operations encoded in the group presentation, we also need to consider the global operation of ‘remove a string from the left and append it to the right’.
Gabriel remarked that if xy = e, then yx = e (where e is the identity) and therefore it is impossible to convert an identity necklace into a non-identity necklace or vice-versa, solving the original problem. However, it doesn’t solve the problem of whether we can convert between BBB and WWWW, since these are both non-identity necklaces. However, thinking for a moment results in the following observation.
-
yx = y xy y’
Here y’ is the inverse of y. So, we can think of moving the string y from the left to the right as conjugating by y. Indeed, this operation of rotating the beads on the necklace is precisely the same operation as conjugation: no more; no less. This leads to this rather neat conclusion:
We can convert between two necklaces if and only if they are in the same conjugacy class.
Christmas generalisation
Gabriel attempted to construct similar problems based on other groups. I mentioned how the dihedral groups have relatively small group presentations, and this is the smallest non-trivial example. Eventually, I suggested the following problem:
We have three types of bead (red, gold and forest green, to make this problem nice and festive!), and are allowed the following operations:
-
Insertion or deletion of five consecutive red beads;
- Insertion or deletion of three consecutive gold beads;
- Insertion or deletion of two consecutive green beads;
- Replacing a red-gold (in clockwise order!) pair with a green bead, or vice-versa.
Then, a nice problem is to determine necessary and sufficient conditions for it to be possible to convert a necklace of m red beads into a necklace of n red beads. Also, you may want to work out which group underlies this problem (the answer is nice and simple!), and how many conjugacy classes it possesses; post your solutions in the ‘comments’ section at the bottom of this post.
Problems, books and quotations
Anyway, Gabriel’s solution is what Paul Erdős would call a proof from the book, meaning that it is clearly the right way to think about the problem. I particularly like this problem from the Advanced Mentoring Scheme, which has a horribly ugly case-bash official solution as well as a beautiful proof from the book. See if you can find the latter (again, post your solutions as comments on this article):
A class of students takes eight exams of which each student passes exactly four. For each pair of students, there are precisely two exams passed by the first and not the second, and precisely two passed by the second and not the first. What is the maximum possible size of the class?
Completely coincidentally, whilst checking my e-mails to find the exact verbatim statement of the AMS problem, I have just received one from Gabriel entitled ‘positive consequence of cp4space’ explaining how he used the Cayley-Bacharach theorem to solve question G6 on the 2006 IMO shortlist. Again, this is shorter and more elegant than the official solutions, although I wouldn’t go as far as saying that this was a proof from the book (a term generally associated with using more advanced theory than is necessary to understand the problem). Indeed, Erdős believed that God has a book containing the most elegant proof of each theorem.
More generally, Erdős famously used rather colourful terminology to refer to various concepts. They are mentioned in this delightful comic by Mike. Nevertheless, I suppose that my favourite amusing quotation by a great mathematician is this one of Hilbert’s:
A mathematician should have both a wife and a concubine. That way your wife thinks you are with the concubine, the concubine thinks you are with the wife, and finally you have time to do some maths.
(Depending on the gender and sexuality of the mathematician, you may need to replace ‘wife’ with ‘husband’. I think that concubine is technically gender-neutral.)
More mathematical quotations can be found on MathOverflow.

I think I have an answer to exams question: 7. I don’t think this is the case-bash solution you mentioned, because I rather just throw out most of possibilities.
1 denotes passed exam, 0 failed one. WLOG, let the first student pass exactly the first four exams: 11110000. Now all following students must have passed exactly two of first four exams. Suppose three of them had same results, let’s say 1100. If on latter four first of students passed 1100, others must have had 0011. But now second and third students passed exactly same exams. So at most 2 students got same results on first 4 exams.
Now suppose 3 students have results starting with 1100 or 0011. Two of them had same results (pigeonhole principle), WLOG say they had 1100. We know other one couldn’t have 1100, so he had 0011. So in latter 4 exams, he had both of passed exams same as first two students. But they must’ve had opposite scores, so it’s impossible.
So at most 2 students had scores beginning with 1100 or 0011. Similarily for 1010 and 0101 and for 1001 and 0110. So, if we add our first student with 11110000 we get upper bound of 7 students, which can be attained, e.g. by following example:
11110000/11001100/11000011/10101010/10100101/10011001/10010110
It’s a bit lengthy solution, but idea is rather simple.
7 is indeed correct, and your proof is valid, but there’s a much nicer way to prove the upper bound of 7.
Hint: use +1 and -1 instead of 1 and 0, and think of these as vectors in . Then what can you say about the resulting vectors, and why does this instantly give you the answer?
. Then what can you say about the resulting vectors, and why does this instantly give you the answer?
Hmm, I don’t know how obvious things I’m missing, but only thing I came up with is that if we take two vectors and multiply corresponding numbers we get a vector which is consistent with these two (according to our problem). Other than that, I seem to not know enough about vectors.
The first condition (each student passes 4 and fails 4) means that the sum of elements (or equivalently the dot product with (1,1,1,1,1,1,1,1)) is zero, thus the vectors lie in a 7-dimensional subspace.
The second condition means that any two students are orthogonal to each other (the dot product is zero), and we can only find seven mutually orthogonal vectors in a 7-dimensional subspace.
I’ve been working on G6 on the IMO 2006 shortlist for a while and I can’t seem to figure out how Cayley-Bacharach generates a more elegant solution. The best I could do was to use Cayley-Bacharach in place of Pappus’s Theorem in Solution 2 which lets me prove that AO_1, BO_2, and EF are concurrent; but showing that the point also lies on the line t eludes me. Besides Menelaus in Solution 1 or the homothety in Solution 2, is there a clean way to show that t contains the point in question?
Here’s the solution that Gabriel sent me:
Let X be the intersection of AO1 and EF. By homothety, EDB and FDA are both lines; trivially EO1O and FO2O are also lines. Then my three conics are:
EXF union O1DO2 union AOB
EO1O union XO2B union FDA
EDB union O1A union FO2O
Hence X is on O1A by Cayley Bacharach.
Now AFB = AEB = 90 so AE, FB and t concur at Z. O1O2 and EA meet at A’; by homothety A’ is on omega 1. Define B’ similarly. Now O1D/DO2 = A’D/DB’ = AY/YB (because, being simultaneously perpendicular to t, O1O2 and AB are parallel), so XDY are collinear, and t passes through X as required.
Okay, the first part is basically Pappus as in Solution 2 (although I do find Cayley Bacharach to be easier to apply than Pappus), but the second part does seem to be cleaner than either of the approaches in the official solution. That’s pretty cool.