As I’ve mentioned before, a snark is a 3-regular bridgeless graph which cannot have its edges 3-coloured such that each vertex is incident with one edge of each colour. One particular example is curiously named the Descartes snark, and is based on the Petersen graph.
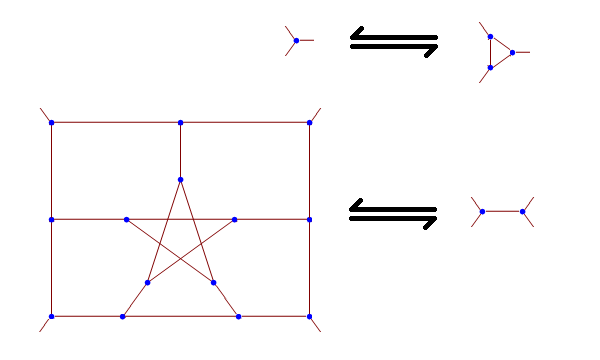
The Descartes snark has 210 vertices, and can be described by beginning with the Petersen graph and applying operations that are guaranteed to convert one snark into another. For example, a single vertex can be replaced with a triangle of vertices, with the original graph being 3-edge-colourable if and only if the new graph is 3-edge-colourable; the contrapositive is that this transforms a snark into a different snark.
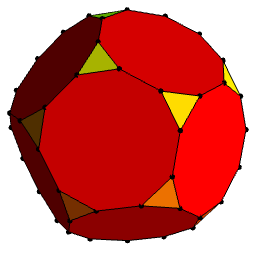
Applying this simultaneously to every vertex of the Petersen graph results in the skeleton of a truncated hemi-dodecahedron. This is the projective polyhedron obtained by identifying antipodal features of the truncated dodecahedron:
Some authors insist that a snark be triangle-free, so this is a slightly degenerate example.
The second transformation is more complicated. Concentrate on the large object, and suppose we have a 3-edge-colouring. After a short case bash (hint: consider the possible 3-edge-colourings of the central ‘star’, and extrapolate from there), one can see that the two edges emanating from the left must be the same colours (in some order) as the two edges emanating from the right, and these two edges must have distinct colours.
Hence, this ‘gadget’ is equivalent to a single edge between two vertices. In fact, the Petersen graph itself can be obtained by starting from a degenerate snark (an edge between two vertices with self-loops), applying this transformation, and then contracting the two triangles which result. But, anyway, if we gratuitously apply this operation to all of the 15 original edges of the Petersen graph present in our truncated hemi-dodecahedron, then the triangles are expanded out into nonagons and the snark is no longer degenerate:

Image courtesy of Gabriel Drummond-Cole
This is the Descartes snark. But why is it called the Descartes snark? René Descartes massively predated graph theory, so clearly he did not discover it. Alternatively, it may have been named in his honour, but it transpires that the truth is much more interesting. Indeed, it was not named after René at all, but rather after a certain Blanche Descartes.
Blanche discovered the snark in 1948. One would imagine that she made the same observation that the gadget behaves identically to a single edge, and thus realised that there are, in fact, infinitely many snarks obtainable by iterating the process of truncating vertices and replacing the original edges with meta-edges.
Anyway, when I say ‘she’, there is a slight caveat: Blanche is not an individual, but rather a collective comprising Bill Tutte, Leonard Brooks, Arthur Stone and Cedric Smith (the four legendary Trinity mathmos responsible for squaring the square). They concatenated their first initials to form BLAC, which is not a name, but easily augmentable to ‘Blanche’ by the insertion of additional letters. As for the surname, this was a clever pun on the phrase carte blanche (which transliterates as ‘blank paper’, and refers to an open agreement).
As mentioned in this article, Blanche Descartes (who is undoubtedly the oldest female Trinity mathematician) also published several poems in addition to her theorems, including one to celebrate the wedding of the daughter of the (equally fictional) Nicholas Bourbaki. Despite this, the four mathematicians were meticulously careful in not revealing the non-existence of Blanche Descartes…

1. Is the edge between two vertices with self-loops technically a snark? It doesn’t look bridgeless.
2. Defining “snark” to be any non-three-colorable graph, note that the two operations in this article can be used to define an equivalence partition on graphs where two are equivalent if they can be transformed into one another by a finite sequence of applications of the operations. If infinite graphs are allowed, there must be at least one partition per cardinal, and the partitions are a proper class. If we restrict our attention to finite graphs, though, how many equivalence classes are there? At least one equivalence class of snarks and one of non-snarks must exist, so it is at least two. Is it exactly two? Are all snarks equivalent? Are these questions even answered as of yet?
3. I’d heard of Bourbaki before, but not Blanche Descartes. How many other mathematicians are/were also actually collectives sharing a pseudonym, that we know of?
1. No, it’s very highly degenerate, and is indeed not bridgeless.
2. The operations cannot alter the number of connected components, so infinitely many equivalence classes of non-snarks exist. Also, girth-6 snarks cannot be obtained from the Petersen graph by these operations, so there are at least two (probably infinitely many) equivalence classes of snarks.
3. I have no idea.
Interesting. How many equivalence classes of connected non-snarks?
Please consider the above amended to restrict section 2 to 3-regular graphs. Obviously, there are lots of equivalence classes when other graphs are included — every n-regular graph for n != 3 becomes a one-element one since neither transform is applicable, at least not if interpreted strictly as requiring all involved vertices to be trivalent.