Several rather interesting developments have occurred this month. In inverse chronological order, they are summarised below:
E8 and Λ24 lattices actually are optimal
The lattices E8 and Λ24 are lattice packings of unit spheres in 8 and 24 dimensions, respectively. They possess many exceptional properties, including being highly symmetrical and efficient sphere packings. Indeed, it was shown that, among all lattice* packings of spheres in 8 and 24 dimensions, E8 and Λ24 have the highest density. Moreover, it was known that no packing whatsoever could be more than microscopically more efficient than either of these exceptional lattices.
*that is to say, ones where the group of translational symmetries acts transitively on the set of spheres.
Now, it has actually been proved that E8 and Λ24 have the highest density among all sphere packings, not just lattice packings. Maryna Viazovska made a breakthrough which allowed her to prove the optimality of the 8-dimensional packing; subsequently, she led a group of collaborators who refined this approach to apply to the 24-dimensional Leech lattice.
More on this story here.
AlphaGo defeats Lee Sedol in a 4-1 victory
A team of researchers at Google DeepMind developed a program to play the board game Go at the professional level. It was pitted against a 9-dan professional Go player (that is to say, one of the very best Go players in the world), Lee Sedol, winning four of the five matches. Lee Sedol was able to obtain a single victory, his fourth game, by observing that AlphaGo was less strong when faced with unexpected moves (despite having made several of its own, described by spectators as ‘creative’!).
The algorithm ran on a distributed network of 1202 CPUs and 176 GPUs. It uses a combination of brute-force tree searching (like conventional chess algorithms), Monte Carlo simulations (where many plausible futures are simulated and evaluated) and pattern recognition (using convolutional neural networks). These convolutional neural networks are much larger and deeper than the one I implemented on the Analytical Engine, with 192 feature-maps in the first convolutional layer. In particular, AlphaGo used:
- A value network to evaluate how favourable a position appears to be;
- A supervised policy network to learn how a human would play;
- A reinforcement policy network to decide how it should play;
- A fast rollout policy network which is a simpler, cruder, and faster counterpart of the above (used for the Monte Carlo rollouts).
The supervised policy network was trained on a huge database of human matches, learning to recognise spatial patterns with its convolutional networks. After quickly exhausting the database, it had no option but to play lots of instances of itself via reinforcement learning, using competition and natural selection to evolve itself. In doing so, AlphaGo had effectively played more matches than any human had ever seen, growing increasingly powerful over a period of several months (from when it played the 2-dan European Go champion Fan Hui).
A much more detailed description of the algorithm is in the Nature paper.
Unexpected pattern discovered in Conway’s Game of Life
It transpires that, despite 46 years of interest and hundreds of thousands of CPU-hours of Monte Carlo searching, there was a piece of low-hanging fruit in an area no-one had thought to explore. This was the copperhead, a spaceship with the unusually slow speed of c/10:

Alexey Nigin wrote an excellent article describing its discovery. In the next few days after the article’s publication, there were additional breakthroughs: Simon Ekström discovered that the spaceship could be extended to produce a profusion of sparks:

This extension is capable of perturbing passing objects, such as reflecting gliders. A convoy of these creatures can consequently catalyse more complex interactions, such as duplicating and recirculating gliders to yield an unterminating output; the following example was constructed by Matthias Merzenich:
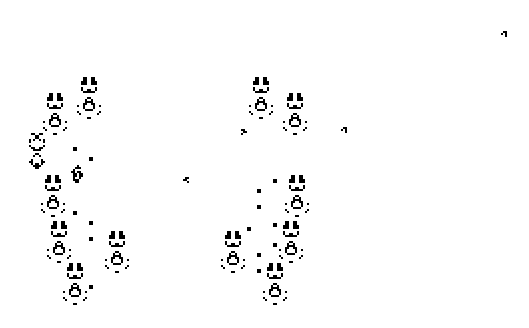
As you can see, there is a steady stream of NE-directed gliders escaping to the right.

Could you also provide RLE files of these patterns?
The RLE for the copperhead+tagalong is:
x = 8, y = 18, rule = B3/S23
b2o2b2o$3b2o$3b2o$obo2bobo$o6bo2$
o6bo$b2o2b2o$2b4o2$3b2o$2bo2bo2$
bo4bo$2o4b2o$bob2obo$2b4o$3b2o!
and the original c/10 can be recovered by detaching the back.
+1 for the Guy Fawkes phase
Pingback: AlphaGo Zero | Complex Projective 4-Space