There has been further recent activity on the Chromatic Number of the Plane problem, with an eleventh research thread being spawned. Philip Gibbs has been able to 6-colour a large disc (with diameter slightly greater than 4), and Aubrey de Gray has remarked that it can be enlarged slightly further still:
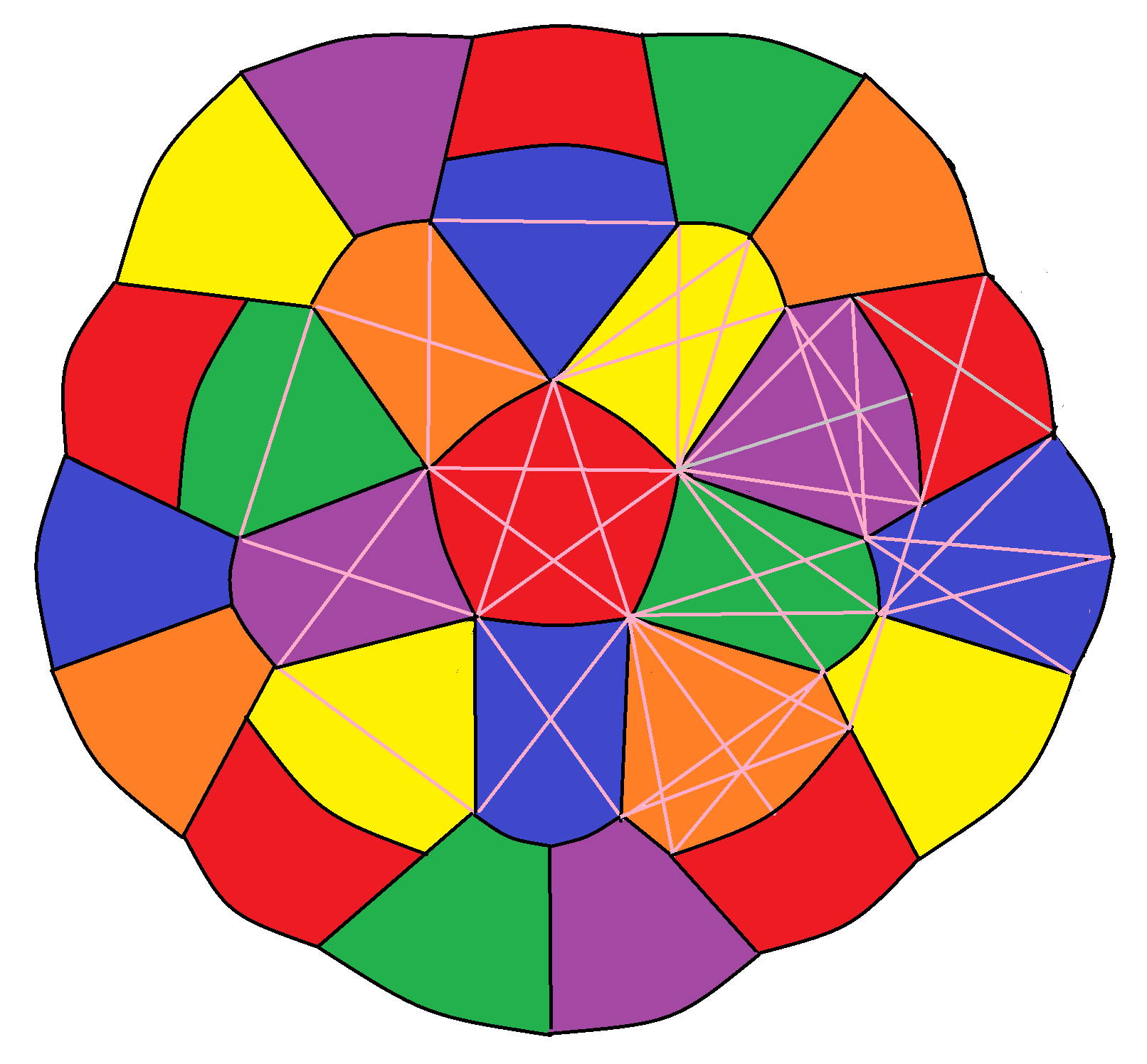
An infinite strip of width 
What about the whole plane?
Interestingly, it has been shown that any tile-based 6-colouring of the plane is critical in the sense that the maximum diameter of any tile must be equal to the minimum separation between similarly-coloured tiles; there is no room for manoeuvre. Moreover, this means that it is insufficient to simply specify the colours of the tiles themselves; it is necessary to also colour the (measure-0) vertices and edges where they meet!
More updates as events warrant…
“it is insufficient to simply specify the colors of the tiles themselves; it is necessary to also color the (measure-0) vertices and edges where they meet!” That’s wrong, actually. Someone (maybe Terry Tao) had a very clever argument early on in the discussions that, if you can k-color the plane except for a set of measure 0, then you can k-color the plane.
I can’t find the argument to link to right now, but I remember it: Let U be a subset of R^2 whose complement has measure 0, such that the unit distance graph of U can be k-colored. Let G be any finite unit distance graph. Then a random translate of G will, with probability 1, lie in U. So G can be k-colored. But the De Bruijn–Erdos theorem states that, if every finite subgraph of a graph can be k-colored, then the whole graph can be k-colored. So this would show that the unit distance graph of R^2 can be k-colored.
That’s a beautiful proof! Observe that the resulting k-colouring of the plane is no longer guaranteed to be tile-based, though, so it’s entirely possible that the following are simultaneously true:
(a) There exists a tile-based 6-colouring of an open subset of R^2 with measure-0 complement;
(b) There does not exist a tile-based 6-colouring of R^2;
(c) There does exist a nonconstructive 6-colouring of R^2 (assuming choice).
The proof you mentioned entails (a) –> (c), but not that (a) –> ¬(b).