The previous post ended with unanswered questions about describing the Conway group, Co0, in terms of quantum gates with dyadic rational coefficients. It turned out to be easier than expected, although the construction is much more complicated than the counterpart in the previous post.
We’ll start with a construction for a much smaller simple group — the order-168 group PSL(2, 7) — which can be generated by three CNOT gates acting on the three lower qubits in the diagram below:
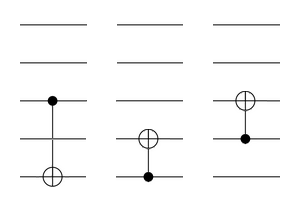
For the moment, ignore the two unused upper qubits; their purpose will become clear soon enough. The three lower qubits have eight computational basis states (000, 001, 010, 011, 100, 101, 110, and 111). Viewing each of these states as a three-dimensional vector over , the CNOT gates induce linear shearing maps (and together generate the full 168-element group of linear automorphisms).
Now we introduce another two CNOT gates:
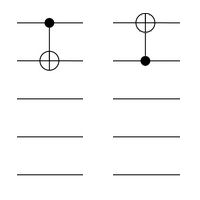
These act only on the two upper qubits, and generate the symmetric group (freely permuting the states 01, 10, and 11). These two gates, together with the three gates in the previous diagram, therefore generate the direct product
of order 1008.
It is helpful to partition the 32 computational basis states into four 8-element sets:
- the set W consisting of all basis states of the form 00xyz;
- the set A consisting of all basis states of the form 01xyz;
- the set B consisting of all basis states of the form 10xyz;
- the set C consisting of all basis states of the form 11xyz;
where x, y, z are elements of {0, 1}. Then the two gates on the upper qubits are responsible for bodily permuting the three sets {A, B, C}; the three gates on the lower qubits induce the same linear permutation in each of W, A, B, and C (viewed as 3-dimensional vector spaces over the field of two elements).
Note that the permutation group is transitive on the 8-element set W, and transitive on the 24-element set V (the complement of W, or equivalently the union of A, B, and C), but no elements of V are ever interchanged with elements of W. This will remain the case as we continue to add further gates.
For the time being, we’ll therefore suspend thinking about the smaller 8-element set W, and concentrate on the larger 24-element set V.
We now introduce a sixth CNOT gate, bridging the upper and lower qubits:
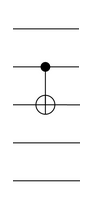
This now expands the size of the group by a factor of 64, resulting in a 64512-element group called the trio group. The vector spaces A, B, and C are effectively upgraded into affine spaces which can be semi-independently translated (the constraint is that the images of their ‘origins’ — 01000, 10000, and 11000 — always have a modulo-2 sum of zero).
The trio group, considered as a permutation group on the 24 basis states in V, is a maximal subgroup of the simple sporadic group M24. That means that adding a single further gate to break out of the trio group will immediately upgrade us to the 244823040-element Mathieu group! Unfortunately, I wasn’t able to find a particularly simple choice of gate:
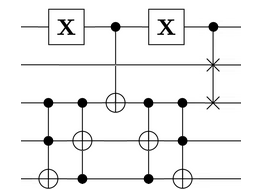
The effect of this complicated gate is to do the following:
- Within each of the sets W and A, apply a particular non-affine permutation which exchanges the eight elements by treating them as four ‘pairs’ and swapping each element with its partner:
- 000 ⇔ 100;
- 001 ⇔ 110;
- 010 ⇔ 111;
- 011 ⇔ 101;
- Swap four elements of B with four elements of C by means of the Fredkin gate on the far right.
In terms of its action on V, this is an element of M24, but does not belong to the trio group. Interestingly, it belongs to many of the other important subgroups of M24 — namely PSL(3, 4) (also called M21), the ‘sextet group’, and the ‘octad group’. At this point, the group generated by these seven gates is now the direct product of the alternating group A8 (acting on the set W) and the Mathieu group M24 (acting on the set V).
The elements of the Mathieu group are permutations on the set V, which can be viewed as 24-by-24 permutation matrices. Permutation matrices are matrices with entries in {0, 1}, where there’s exactly one ‘1’ in each row and column. If we throw in a Z-gate acting on the uppermost qubit, we’ll expand this to a group 212:M24 of ‘signed permutation matrices’ instead, where some of the ‘1’s are replaced with ‘−1’s. (The sets of rows and columns containing negative entries must form codewords of the binary Golay code; this is why each permutation matrix has only 212 sign choices instead of 224.) This group is interesting inasmuch as it’s the group of permutations and bit-flips which preserve the binary Golay code. It’s also a maximal subgroup, called the monomial subgroup, of the Conway group Co0.
Instead of using this Z-gate, we’ll bypass the monomial subgroup and jump straight to the Conway group by adding a single additional three-qubit gate:

By a slight abuse of notation, we’ll reuse the symbols W and V to refer to the vector spaces spanned by first 8 basis states and final 24 basis states, respectively. After introducing this final gate, the resulting group of 32-by-32 matrices is a direct product of:
- an order-348364800 group (the orientation-preserving index-2 subgroup of the Weyl group of E8) acting on the 8-dimensional vector space W;
- an order-8315553613086720000 group (the Conway group, Co0) acting on the 24-dimensional vector space V.
These are the groups of rotational symmetries of the two most remarkable* Euclidean lattices — the E8 lattice and the Leech lattice, respectively. Indeed, if we take all linear combinations (with integer coefficients!) of the images (under the group we’ve constructed) of a particular computational basis state, then we recover either the E8 lattice or the Leech lattice (depending on whether we used one of the basis states in W or in V).
* as well as being highly symmetric, they give the optimal packings of unit spheres in 8- and 24-dimensional space, as proved by Maryna Viazovska.
These two groups each have a centre of order 2 (consisting of the identity matrix and its negation), modulo which they’re simple groups:
- the quotient of the order-348364800 group by its centre is PSΩ(8, 2);
- the quotient of Co0 by its centre is the sporadic simple group Co1.
This process of quotienting by the centre is especially natural in this quantum gate formulation, as scalar multiples of a vector correspond to the same quantum state.
Further connections
If we take qubits and the gates mentioned in the previous post, we remarked that the group generated is the full rotation group
. If instead we replace the Toffoli gate in our arsenal with a CNOT gate, we get exactly the symmetry groups of the Barnes-Wall lattices! The orders of the groups are enumerated in sequence A014115 of the OEIS.
Acknowledgements
Thanks go to Conway and Sloane for their magnificent and thoroughly illuminating book, Sphere Packings, Lattices, and Groups. Also, the website jspaint.app (which is undoubtedly the most useful thing to have ever been written in JavaScript) was helpful for creating the illustrations herein.

Pingback: Minimalistic quantum computation | Complex Projective 4-Space
Pingback: An attempt to understand the Monster group | Complex Projective 4-Space