Tomasz Kania and I recently coauthored a paper about Banach spaces. The paper makes extensive use of the axiom of choice, involving a transfinite induction in the proof of Theorem B as well as several appeals to the fact that every vector space admits a Hamel basis.
The axiom of choice is often misunderstood, as is many of its consequences. I often hear the Banach-Tarski ‘paradox’ being quoted as a philosophical argument against the truth of the axiom of choice. However, the statement of the Banach-Tarski theorem is not paradoxical at all. One way to state Banach-Tarski is:
- The set of points in a closed unit ball can be rearranged into the disjoint union of two copies of the set of points in a closed unit ball through a finite sequence of operations of splitting a set [into a disjoint union of two subsets], rotating a set, translating a set, and recombining two disjoint sets into their union.
Note that the set of points in a closed unit ball is an [uncountably] infinite set. We are perfectly accustomed to the points in an infinite set being in bijective correspondence with two copies of the original set: for instance, the even integers and the odd integers are each isomorphic to the integers. So we could write the following uncontroversial statement which differs from the Banach-Tarski theorem in only the indicated locations:
- The set of integers can be rearranged into the disjoint union of two copies of the set of integers through a finite sequence of operations of splitting a set [into a disjoint union of two subsets], applying an affine transformation to a set, and recombining two disjoint sets into their union.
In particular, we split the integers into the odd integers and the even integers, and affine-transform each of these sets into a copy of all of the integers. This is uncontroversial, and doesn’t require the axiom of choice. No-one would non-ironically argue that this implies the arithmetic statement 1 = 1 + 1, because it is intuitively obvious that the set of integers is infinite and that the only statement about cardinals that this immediately implies is that ℵ_0 = ℵ_0 + ℵ_0.
However, people often feel differently about the Banach-Tarski ‘paradox’ because a closed unit ball feels like a tangible solid object. It is often joked that the Banach-Tarski paradox can be used to duplicate approximately-spherical real-world objects, such as oranges, as was the subject of this rather bizarre music video:
Notwithstanding any physical intuition, a closed unit ball is nonetheless an uncountable set of points. The axiom of choice merely gives us extra freedom in manipulating certain infinite sets and is particularly useful for constructions that involve induction over uncountable sets.
The Banach-Tarski theorem is still mathematically interesting and nontrivial, unlike the statement we made about rearranging the integers. It proves that there is no translation-invariant rotation-invariant finitely-additive measure on (n >= 3), whereas such a measure does exist in n = 2 dimensions as proved by Banach.
The proof of Banach-Tarski is even more interesting than the statement, and is well worth reading. It relies on the fact that the free group on two generators can be embedded as a subgroup of SO(n) when n >= 3; this is not the case for n = 2.
But what Banach-Tarski certainly does not imply is this nonsense*:

A misunderstanding of Banach-Tarski
(*ordinarily I would be more polite when someone is wrong on the internet, but the author of this tweet has been engaging in a highly dubious trolling campaign. Tim Gowers has weighed in on the discussion with an informative thread.)
The constructible universe
There’s actually a more fundamental reason why the axiom of choice cannot possibly be blamed for any results in arithmetic, false or otherwise. Assuming ZF set theory, then inside the von Neumann universe V is a subclass** (which may or may not be the whole of V) called L, also known as Kurt Gödel’s constructible universe.
**like a subset, but too big to be a set in the set-theoretic sense of the word set.
L is very well-behaved. Firstly, it is an internally consistent model of ZF set theory. Moreover, this operation of taking the constructible universe is idempotent: if we take the constructible universe within L (instead of within V), we still get the whole of L. This means that L is a model of V=L, together with anything that logically follows from V=L such as the axiom of choice or the Generalised Continuum Hypothesis. That is to say that L unconditionally satisfies the axiom of choice even if the full universe V does not.
Finally, and importantly for us, the Shoenfield absoluteness theorem states that certain statements (namely those that are at most Σ^1_2 or Π^1_2 in the analytical hierarchy, which subsumes all statements in first-order Peano arithmetic) are true in V if and only if they are true in L.
In particular, if a statement about first-order Peano arithmetic is proved in ZFC, then the result is also true in ZF (because you can ‘run the proof inside L’ where the axiom of choice holds, and then use the Shoenfield absoluteness theorem to transfer the result back to V). Indeed, you can also freely assume anything else that follows from V=L, such as the truth of the Generalised Continuum Hypothesis. This meant that reliance on the axiom of choice could easily be removed from Wiles’s proof of FLT, for instance.
If the author of that tweet or anyone else managed to prove 2+2=5 using ZFC, then the proof could be modified to also operate in ZF without requiring choice. This would, of course, mean that ZF is inconsistent and mathematics would reënter a state of foundational crisis.
Anyway, this is something of a distraction from the main purpose of this post, which is to briefly discuss one of the many*** useful applications of the axiom of choice.
***other applications include proving Tychonoff’s theorem in topology, the compactness theorem for first-order logic, the existence of nontrivial ultrafilters, that every vector space has a Hamel basis, et cetera.
Transfinite induction
One equivalent form of the axiom of choice is that every set can be bijected with an ordinal. Ordinals have the property that every non-empty subset of an ordinal has a least element, which makes them ideal for inductive proofs: if you want to prove that a property P holds for all elements, you need only show that there isn’t a least counterexample.
An application of this is to be able to perform a step-by-step construction involving uncountably many ‘steps’. For example, a fun question is:
Can three-dimensional space be expressed as a union of disjoint circles?
Using a transfinite induction, it is possible to place each of the uncountably many circles one at a time, avoiding any previous circles and ensuring that every point in the ambient space has been accounted for. Peter Komjath described such a construction in an answer to the question when it was asked on MathOverflow:

It is worth emphasising that this uses the least ordinal of cardinality continuum. These ‘initial ordinals’ have the useful property that all previous ordinals are strictly smaller from a cardinality perspective. This means that at each stage in the transfinite induction, the number of circles that have already been emplaced is strictly lower than the cardinality of the continuum, so there’s plenty of room to insert another circle passing through a specified point. This same idea was used in the paper I coauthored with Tomasz Kania.
A generalisation of this problem which remains open is whether there exists such a partition where every pair of circles is pairwise linked. The Hopf fibration provides a solution where is augmented with an extra point at infinity, where every pair of circles interlock in the same manner as these two rings of dodecahedra:
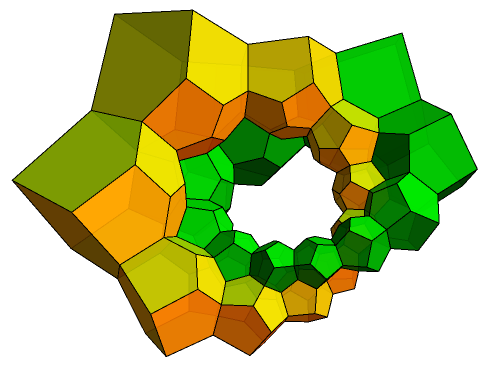
Without this point at infinity, though, the problem is much harder and has evaded solution. Transfinite induction can show that we can cover all but one point with disjoint linked circles, but there is no easy way to modify the proof to cover the last point.
