Digest

There have been several recent items of news, either related to or inspired by the recent postings on Complex Projective 4-Space. Rather than mention them separately, I have collected them in this ‘digest’ format.

Jigcypher solved

I received an anonymous e-mail from someone who solved the Jigcypher using a computer program. He/she (according to the Gender Genie software, he) subjected my Jigcypher to the program, which successfully assembled about 88% of the pieces. After completing the jigsaw puzzle manually, it wasn’t long before the cipher itself was also solved.

It transpires that he made the program earlier to reconstruct shredded documents. There is even commerical software out there designed to do this. I imagine this could be invaluable to archaeologists attempting to assemble fragments of the Dead Sea Scrolls and other ancient documents, as well as of interest to organisations such as the CIA.

Katsunobu’s glider

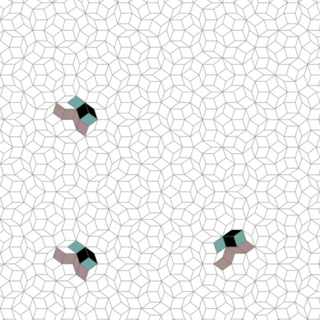
Recently, the second glider on a Penrose tiling was discovered, this time by Katsunobu Imai. Although too late to claim the prize, Imai’s glider is more natural than mine and occurs in a well-known family of cellular automata known as Generations rules. Golly can simulate these rules on an ordinary square lattice, taking full advantage of the HashLife algorithm to achieve exponential speed-up.

Katsunobu’s glider on the P3 Penrose tiling

There is a video and animated GIF of the glider. The glider appears to travel at a speed of c (compared with c/2 for my glider) in the same ten directions. It grows and shrinks according to the underlying tiling, and there is no proof as of yet that the glider will continue forever.

Unlike my glider, it does not function on a kite-and-dart tiling. He attempted to find a glider travelling along an axis of symmetry, but to no avail. It is more likely that there exist natural gliders which imitate mine, moving on convoluted fractal paths with Hausdorff dimension log(6)/log(phi^3).

Professor Andy Adamatzky mentioned that it would be interesting to explore the collisions between gliders on a Penrose tiling. Imai’s rule is more natural, so probably a better environment for investigating rich phenomena.

Myers’ polyhedra

Joseph Myers, inspired by the recent post, constructed card models of the rhombic triacontahedron and hexecontahedron. His construction method was different from mine, avoiding Sellotape to ensure durability. He has a large collection of hand-made card polyhedra.

Joseph Myers’ model of the rhombic hexecontahedron.

Nomography

Although Richard Guy had made a nomogram (an anagram of monogram!) based on a cubic curve, it turns out that it was not equivalent to my elliptic curve calculator. Guy uses a cubic curve of the form y = x^3 + ax + b, which has only a single real point of inflection. Whereas mine emulates a circular slide rule, Guy’s nomogram is equivalent to a linear slide rule. There is also a much simpler explanation for why his works: the abscissae (x-coordinates) of three collinear points on the cubic curve sum to zero.

This idea of using a straight-edge alone to perform calculations lies firmly in the realm of projective geometry. Taking a photograph of a nomogram results in a functionally identical nomogram. There is an 9-parameter family of cubic curves, but only an 8-parameter family of projective transformations. This is why we can have two distinct species of nomograms based on cubic curves: mine and Guy’s.

Miscellany

A mere two days after my hyperbolic eye tessellation, Katie Steckles reported that someone had knitted a Euclidean tessellation in the style of Escher. I commented that this would be compatible with hyperbolic crochet.

Andrew Carlotti found one direction of a closed-form bijection using the inverse Gamma function. He then found a better solution, claiming to have ‘essentially invented the Minkowski Question Mark Function’. Apparently, his latter solution was inspired by origami.