If we provide a bog-standard computer with an infinite data store, it suddenly becomes a Turing machine: capable of answering any question answerable by any digital computer. Even quantum computers are no more powerful; they are merely faster. For example, a quantum computer recently factorised 15 into 5 * 3 by using Shor’s algorithm; an ordinary computer could do this much more slowly by exhaustive search.
Your computer isn’t even as powerful as a Turing machine. Having a mere finite data store, it falls into a weaker class of machines: linear-bounded automata (or LBAs). A linear bounded automaton is just a Turing machine with a large but finite amount of tape. Since we’re so familiar with digital computers, I’ll give examples of other, more unusual, LBAs.
Essentially, to make a LBA we just need to be able to make some simple components and connect them together. I’ll mention a few of the conventional and unconventional approaches here.
Approach 1: Logic gates
This is quite an abstract one. We use Boolean logic operations such as AND, OR and NOT, and have simple components performing each task. For example, the AND gate returns a ‘1’ if both inputs are ‘1’, and ‘0’ otherwise.
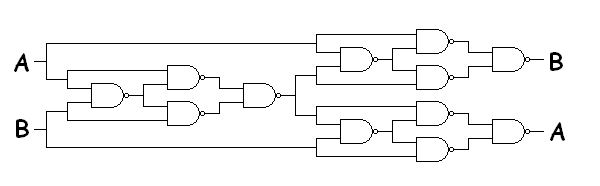
A better logic gate is negative-AND, or ‘NAND’. This inverts the output, so it returns a ‘0’ if both inputs are ‘1’, and ‘1’ otherwise. By connecting up arrangements of NAND gates, we can emulate any other logic circuit. We can even avoid the need for wire crossings by a strategic arrangement of three XOR gates, each composed of four NAND gates:
The inputs are on the left; the outputs are on the right.
Approach 2: Electronic circuits
A conventional way to build computers is to make these logic gates out of electronic components. We currently use CMOS (complementary metal-oxide semiconductor), although earlier versions used conventional transistors and even vacuum tubes. A few years ago I visited Manchester and saw the first stored-program computer. The Baby was built by a team of pioneers, including our favourite, Alan Turing. If you look closely, you’ll see diodes and some larger vacuum tubes called pentodes. No prizes for analysing the Greek stem and ascertaining how many electrodes a pentode has.

The first stored-program computer, housed in Manchester’s Museum of Science and Industry. Click to enlarge.
Of course, there have been earlier computers, including Charles Babbage’s analytical engine, which has yet to be physically constructed. The first computer program (which calculated the Bernoulli numbers) was written by Ada Byron, wife of Lord Byron, who happened to go to the same college as Charles Babbage, namely Trinity College, Cambridge. The web of fundamentally interconnected events never ceases to amaze…
You may believe that our silicon chips represent the most advanced possible electronic circuits, but this is not the case. Transistors have been built from carbon nanotubes, relying on the fact that they can either act as conductors or semiconductors. These nanotube circuits make silicon chips look like vacuum tubes by comparison!
Approach 3: Making logic gates out of sticky mess
Professor Andrew Adamatzky has created logic gates in amazing, unconventional ways. Reaction-diffusion systems (invented by Alan Turing) occur in certain chemical soups, such as the Belousov-Zhabotinsky reaction. This oscillates in colour violently, and causes spirals to emerge. You can investigate these sorts of patterns in the program Ready.
Adamatsky has made similar logic gates using the Plasmodium slime mould. This is a gooey cluster of cells in a much longer life cycle, involving sporangia (like fungi), spores, amoeboids, gametes (some of which have flagellae, like sperm) and zygotes.
Approach 4: Reversible logic
A key feature of the NAND gate is that we can’t reverse it: if a ‘1’ is outputted, the inputs could have either been both ‘0’, or one ‘1’ and one ‘0’. In other words, information is continually lost. An alternative is to use only reversible logic gates. My favourite is the Fredkin gate, which has three inputs (A, B, C) and three outputs (A’, B’, C’). The output C’ is an identical copy of C. The inputs A and B are mapped directly to A’ and B’ (if C is ‘0’) or swapped to B’ and A’ (if C is ‘1’). As such, it is occasionally known as a controlled-swap gate.
The Fredkin gate has three desirable properties:
- Reversibility: given A’, B’ and C’, we can deduce A, B and C. Indeed, the gate is an involution, which means it is equal to its own inverse.
- Conservation: A + B + C = A’ + B’ + C’, which means we can represent the pulses as solid particles.
- Universality: any logic gate can be emulated with Fredkin gates.
The idea led to the concept of a billiard-ball computer, where ‘1’ is represented by a billiard ball and ‘0’ by empty space. Computation is achieved by the balls undergoing elastic collisions with each other. Exactly what the ‘balls’ are is left to your imagination; they could be regular balls, ionised hydrogen atoms, or even planets. Andy Adamatzky has managed to do this with soldier crabs chased by images of predatory birds!
Reversible logic can also be implemented electronically. It is of interest as it can be engineered to produce very little heat, which is the main enemy to the continual miniaturisation of silicon chips.
Quantum computers also use reversible logic gates, but they can exist in a complex superposition of states rather than just one. To emulate a quantum computer on a classical computer, an exponentially large amount of memory is required. For example, a 30-qubit quantum computer requires more than 1000000000 complex numbers to describe its state.
Approach 5: Trains and cellular automata
Instead of logic gates, we can have a single pulse moving around a network of components, storing and reading information. A fun implementation of this is a train on a railway track. It transpires that only three types of points are needed, known as the lazy point, sprung point and flip-flop point. Ian Stewart has a brilliant write-up of this.
I recall that someone even implemented a linear-bounded automaton on the Chalcraft-Greene train set, which was emulated by the Wireworld cellular automaton. There’s an even simpler cellular automaton, Banks-I, which is able to emulate any linear bounded automaton.
The next state of each cell in Banks-I is determined only by that of itself and its four immediate neighbours. Moreover, there are only two states, and the rules are isotropic (reflecting and/or rotating a computer will not affect its operation).
Again, this could have practical applications. There’s an emerging field of ‘quantum-dot cellular automata’, where each cell is a mere 60nm wide. This is superior to existing semiconductor-based circuitry.
What isn’t a linear-bounded automaton?
A Turing machine with infinite memory is more powerful than a linear-bounded automaton. Conversely, if the logic gates ‘burn out’ after a single use, like those in Matt Parker’s domino computer, it is less powerful than a LBA. If something can be ‘solved’ in an amount of time linear in the size of the machine, like the Antikythera mechanism, then it is also weaker than a linear-bounded automaton.

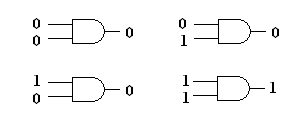

Pingback: NP-triv | Complex Projective 4-Space
Pingback: Three-dimensional chess | Complex Projective 4-Space
Pingback: Circuitry in 3D chess | Complex Projective 4-Space