Continuing the theme of magic squares, we begin with the unique simplest non-trivial magic square. It contains the integers {1, 2, …, 9}, one in each square, such that the rows, columns and diagonals all sum to 15.
Remarkably, the converse is also true. If three distinct integers in the interval {1, 2, …, 9} sum to 15, they form a line in the Lo-shu magic square. This enabled Professor Marcus du Sautoy to demonstrate an equivalent game to tic-tac-toe in the 2006 Royal Institution Christmas Lectures. For convenience, the rules are repeated below:
- There is a ‘bank’, initially containing each of the numbers {1, 2, …, 9}.
- Each turn, a player removes a number from the bank and adds it to his or her inventory. Players alternate turns until the supply is exhausted or someone wins.
- If a player has three numbers summing to 15, he or she wins.
Non-transitive dice
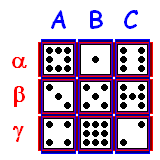
Another property of the Lo-shu magic square is its ability to manufacture non-transitive dice. For each row/column, we make a die by writing each number on two (antipodal) faces. For example, die A is numbered {8,3,4,8,3,4}. Similarly, die B is numbered {1,5,9,1,5,9}.
Alice and Bob have retired from sending secret messages to each other using RSA cryptography, and have decided to play a nice game of dice instead. Simultaneously, Alice throws die A and Bob throws die B. Whoever rolls the higher number wins. As a first approximation, one might imagine that the game is fair, since both dice have the same mean. Further analysis shows that Bob wins 5/9 of the time:
We then introduce a third character, Chris, whose gender is revealed by neither name nor my use of pronouns. Chris rolls die C, marked with the numbers {6,7,2,6,7,2}. Chris beats Bob 5/9 of the time, so one would imagine that die C is optimal and die A is the worst. Surprisingly, Alice beats Chris 5/9 of the time, so this new game is completely balanced! It is similar to the popular game of rock-paper-scissors.
This situation is mirrored by the dice α, β and γ. Due to the difficulty of incorporating Greek letters into blog posts, we’ll concentrate without loss of generality on their Roman counterparts.
Generalising to five dice
Sam Kass and Karen Bryla augmented the traditional game of Rock, Paper, Scissors to encompass two new entities: Lizard and Spock. I was very fortunate to find that my naïve magic square construction generalises to produce a set of five non-transitive dice with cyclic symmetry.
My five dice (which can be implemented as icosahedral dice, since 5 divides 20) are given below:
- Rock: {1,7,13,19,25}
- Paper: {15,16,22,3,9}
- Scissors: {24,5,6,12,18}
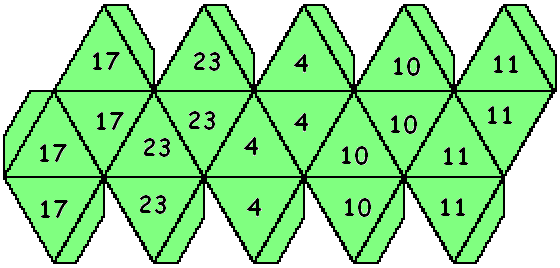
- Lizard: {17,23,4,10,11}
- Spock: {8,14,20,21,2}
It is a remarkable fact that these dice do indeed emulate the game, i.e. die X has a probability greater than ½ of winning against die Y if and only if X beats Y in the game. Specifically, we have the following:
- Paper disproves Spock with a probability of 14/25;
- Spock dematerialises Rock with a probability of 14/25;
- Rock blunts Scissors with a probability of 14/25;
- Scissors decapitate Lizard with a probability of 14/25;
- Lizard eats Paper with a probability of 14/25;
- Paper smothers Rock with a probability of 13/25;
- Rock crushes Lizard with a probability of 13/25;
- Lizard poisons Spock with a probability of 13/25;
- Spock smashes Scissors with a probability of 13/25;
- Scissors cut Paper with a probability of 13/25.
Here’s a net of the Lizard die, obtained by writing the numbers in a straightforward way on the net of an icosahedron.
If I ever visited the Gathering for Gardner, I would probably give away sets of these five non-transitive icosahedral dice as exchange gifts.


Pingback: Markov basket-weaving | Complex Projective 4-Space
Now there are really Rock Paper Scissors Lizard Spock Dice.
Look them up on BoardGameGeek.com.
Pingback: Tournament dice | Complex Projective 4-Space
I managed to find a set of three dice that each beat the next with a probability of 9/16. Is the maximal probability for three dice known?