The Labyrinth usually refers to a particular maze in Knossos on the Greek island of Crete, designed by Daedalus to contain the Minotaur: a ravenous bull-human hybrid, which found human sacrifices particularly appetising. Theseus navigated these tortuous underground passageways by means of a ball of luminous thread given to him by Ariadne.
Mazes come in a variety of shapes and sizes. Topologists can distinguish between mazes by their genus: vaguely speaking, the number of ‘loops’ in it. A genus-0 maze is known as simply connected, as there is only one path from the entrance to any other point. We can count the number of simply connected mazes in a given bounding box by means of Kirchhoff’s theorem, which forms the basis of a programming challenge on Project Euler.
A more traditional problem is to solve a maze. For simply connected mazes, there is only one solution. Multiply connected mazes have several paths from the entrance to the exit; typically the shortest route is desirable. There exist several algorithms capable of this, the most famous of which is Dijkstra’s algorithm. Another method, the breadth-first search, is implemented as a cellular automaton available from the Rule Table Repository. This is not unlike the luminous thread approach favoured by Theseus.
Now that I’ve rambled on about mazes for too long, here’s a maze-cipher combo for you to solve.
Enjoy!

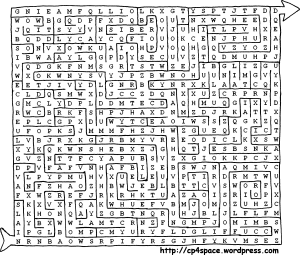
Solved using Mathematica – there’s an interesting series of posts on the Wolfram blog which go into maze solving in some depth. For the cipher cracking I used my Delphi cipher suite, written ages ago.
Oh, awesome, I do practically everything (including creating that array of letters that forms the maze) using Mathematica as well. That leaves only the third cipher (published today) to remain unsolved.
Did you use optical character recognition or manually input the letters into an array?
I solved the maze by stripping out the letters to obtain a “canonical” maze that looked a lot like http://www.uefap.com/images/maze.gif – then I used Jon McLoone’s graph-based method (thin the maze down to single-pixel paths, then interpret this as a graph where white pixels have edges to white pixels, then run FindShortestPath and convert this back to an image) and superimposed the result onto the original image – the path was quite short so I was perfectly happy to copy the string out by hand. Fun challenge!
Pingback: Markov basket-weaving | Complex Projective 4-Space
An interesting lexicographical point – while in colloquial use, ‘maze’ and ‘labyrinth’ are interchangeable, strictly, they are different things. A maze has many possible paths, of which some may lead to dead ends. By way of contrast, a labyrinth has only a single path – there are no points in a true labyrinth at which you are required to make a choice about which direction to go.
Solved the maze by hand, then used Decrypto to solve the cipher. Thanks!
I did the same as Greg, except that for some reason I tried Vigenere first.