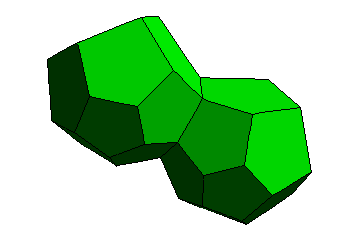
We’ll begin by considering Hamiltonian quaternions, a four-dimensional extension to the complex numbers. A particularly interesting bunch of quaternions is the multiplicative group of 120 ‘icosians’. These can be thought of as the vertices of a 600-cell or, by duality, the centres of the dodecahedra in the 120-cell. The simplest icosian is, without a doubt, 1. Let’s centre a single dodecahedron at 1:
This dodecahedron appears slightly irregular, as I have used a stereographic projection to ‘unravel’ the curved surface of the 120-cell into flat Euclidean 3-space. We’ll consider another icosian quaternion, τ, with the value ½(φ + (1/φ)i + 0j + k). It still has unit length, same as the other 119 icosians, and is quite close to 1. The dodecahedron associated with this icosian is adjacent to the previous dodecahedron:
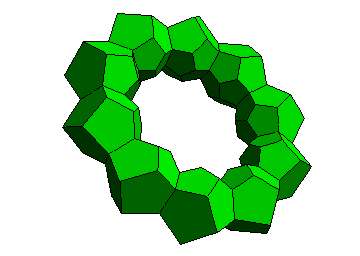
Proceeding logically, we draw dodecahedra at τ^2, τ^3 and so on. As τ^10 = 1, we obtain a closed loop of ten dodecahedra:
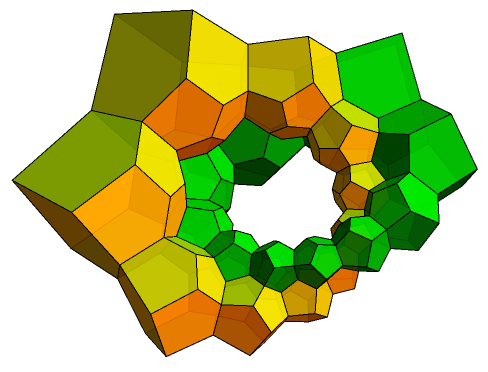
We can multiply the centres of the dodecahedra by another icosian to obtain another ring of dodecahedra. Since they are both great circles, and disjoint from each other, the only possibility is that they are entwined around each other. This is indeed the case:
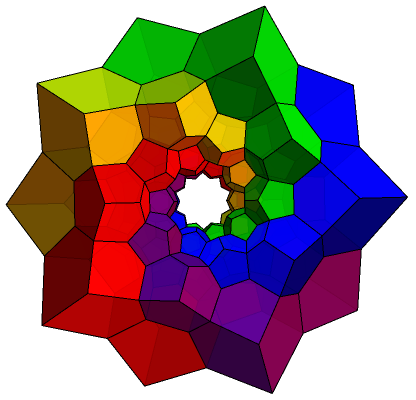
We can repeat this process to obtain more linked rings. Whilst not the typical Olympic Games logo, or indeed the EGMO emblem, here are five linked rings forming a hollow torus capable of accommodating a sixth ring:
By symmetry, each ring in the 120-cell is surrounded by five others, and there are twelve in total. The other structure with this property is the dodecahedron itself: there are twelve pentagons, each of which is surrounded by five others. Is there an explanation for this curiosity?
The Hopf fibration is a bijection between the points on a sphere and a set of intertwining great circles on the surface of a hypersphere. The 120-cell is a tiling of the hypersphere by dodecahedrons just as the dodecahedron is a tiling of the sphere by pentagons. In other words, the interlocking rings of dodecahedra form a discrete Hopf fibration! Similar discrete Hopf fibrations are summarised below:
- 120-cell ↔ dodecahedron
- 24-cell ↔ tetrahedron
- tesseract ↔ dihedron
The dihedron, by the way, is the partitioning of the sphere into two hemispheres. It’s really boring, trivial and degenerate compared with the other regular spherical tilings, the Platonic solids.


Pingback: MODA: Geometry bashing | Complex Projective 4-Space
Pingback: Projective polyhedra | Complex Projective 4-Space
Pingback: Spin groups | Complex Projective 4-Space
Pingback: Treefoil | Complex Projective 4-Space
I your list of fibrations you forgot the 600-cell, which partitions into 20 Boerdijk–Coxeter helices of 30 tetrahedra each. I believe these map to the faces of an icosahedron.
Pingback: Category of scones | Complex Projective 4-Space
Pingback: (W^2 + X^2) / (W^2 + X^2 + Y^2 + Z^2) | Complex Projective 4-Space
I exponentiate T^1 to the T^10 then made stereographic projection of the points. But my points were on a straight line not on a circle. what is my fault?
I also tried this formula (T^1)(*1)*(T^1*) but I get W=1
T^1 multuplication by 1= T^1,
T^1multuplication by it’s conjugate =1 W=1