Wire tetrahedra

Hunter Spink gave me an interesting problem about a beach ball inscribed in a wire tetrahedron, since its most elegant solution uses techniques explored in the tenth chapter of Mathematical Olympiad Dark Arts. Rather than give you the problem now, I’ll keep you waiting eagerly in suspenseful anticipation until MODA is finalised and publicised.

Wireframe polyhedra can do much more than merely circumscribe beach balls. Oh, yes, you can even immerse them in soapy water. When removed, the soap-bubble surface attempts to minimise its energy, and therefore its area. Because it’s easier to think in lower dimensions, consider this analogous problem:

There are plans to build a hyperspace expressway between Earth and three distant locations (assumed to be the vertices of a square of side length 1000 light-years). What is the minimum length of path possible?

Earth and three distant places, positioned at the vertices of a square.

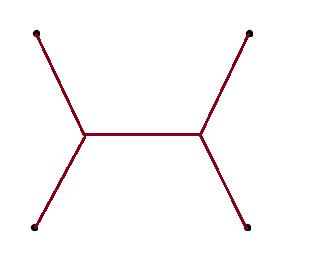
The greedy algorithm is to simply make three edges of the square, with a total length of 3000 light-years. This is sub-optimal, as the two diagonals have a total length of 2828 light-years. Surely that’s optimal?

Actually, no. The most efficient solution (2732 light-years) involves straight line segments meeting at angles of 2π/3, as demonstrated below. You may recognise this as being intimately related to the Fermat-Torricelli point (or first isogonic centre if you’re feeling particularly poncey!) in a triangle, which minimises the sum of distances to each of the three vertices.

In the three-dimensional generalisation, we get four bubble surfaces meeting at a vertex with locally tetrahedral symmetry. I really suggest trying it with an actual wireframe polyhedron in some actual soapy water. Come on, it’ll be fun!

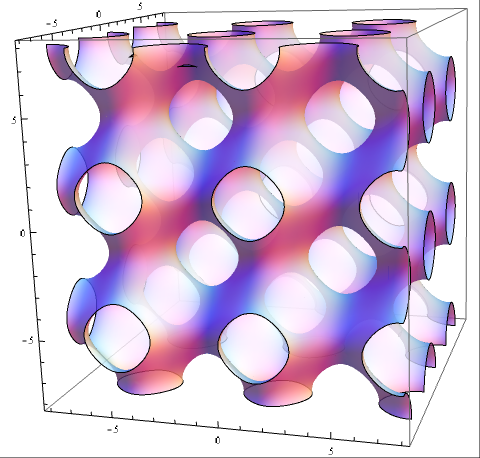
Essentially, soap bubbles obey partial differential equations dictating their curvature. The simplest solution is a spherical bubble, which minimises the area enclosing a given volume. A much more interesting minimal surface (I forget what it’s called — I think it’s the Schwarz P-surface, where P might actually be a different letter) is shown below:

Actually, I’ve cheated and just plotted sin(x) + sin(y) + sin(z) = 0, which is a very close but inexact approximation to the surface.

Conclusion

I can’t think of a way to conclude this post, other than by blowing your mind with the following pearl of wisdom imparted unto me by Richard Freeland last night:

• TRIANGLE is an anagram of INTEGRAL

He also gave four other (less mathematical) anagrams composed of the same eight letters. Can you find them all?