Alexander Betts (nee Luke) posed an interesting problem in combinatorial geometry for the Romanian Masters of Mathematics 2011:
We have a finite set S of n points in the plane, {A1, A2, …, An}, such that (for all i and j) the distances from Ai to all the other points are a permutation of the distances from Aj to all the other points. What possible configurations can S be?
I’ve left it as exercise 17 in chapter 10 of MODA (entitled ‘Areal coordinates’). You may want to think about it before reading on.
The obvious solutions are the vertex sets of regular polygons (which work by symmetry). Upon further consideration, a truncated regular polygon with alternating long and short sides will also work by symmetry. Individual points, lines and rectangles can be regarded as degenerate cases of these.
It turns out that these are the only possible configurations which satisfy the problem. The proof of this involves considering the sum of squares of distances from a particular point to each other point. This is independent of the vertex chosen, by the permutation property. From this and a beautiful result known as the Huygens-Steiner theorem*, we can deduce that the points are equidistant from their centroid, so all lie on a circle. A basic induction then narrows it down to the two types of configuration displayed above.
* If you don’t know it, you can prove it using either Cartesian coordinates (as I did in the competition) or physics (as Jordan did). Thankfully, the rum chocolate bars were just alcoholic enough for us to succeed with these bizarre methods!
Three-dimensional generalisation
The next natural generalisation is into three dimensions. We retain the planar solutions (polygon and truncated polygon) and obtain some more solutions (prisms, antiprisms and twisted prisms) by extending them. Twisted prisms include disphenoid tetrahedra as a special case.
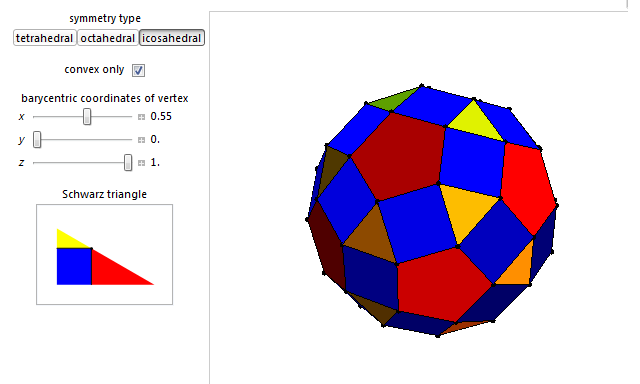
As well as these boring infinite families of solutions, there are some more interesting exceptional cases. The Platonic solids work by symmetry, as do any vertex-transitive polyhedra. They include the Archimedean solids and some slightly deformed versions you can explore with my interactive demonstration:
The are also alternated versions of these, resembling snub dodecahedra, snub cubes and slightly irregular icosahedra (both chiral and achiral versions exist).
Careful consideration (involving plenty of group theory) shows that these are the only finite vertex-transitive arrangements of vertices in three-dimensional space. However, there may be other solutions to the three-dimensional Betts problem, where not all vertices are equivalent but the distances to the others are always permutations. I strongly doubt that they exist. Can you prove that the vertices (which necessarily lie on the surface of a sphere) can only take the aforementioned arrangements, or can you find any counter-examples?

I am able to construct counterexamples in sufficiently large dimensions: sets in Euclidean space where, from each point, the distances to the others are the same, but where the set is not vertex-transitive. I haven’t counted carefully, but I think I need 17 dimensions.
You may wish to have a go yourselves.
Very interesting. I have a construction for ten points in nine-dimensional space, where they are positioned at the vertices of a very slightly irregular simplex. In particular, we let the points be ABCDEFGHIJ, and insist that AB = CD = EF = GH = IJ = 1.00001, AD = BC = EJ = FG = HI = 1.00002, and all other edges have unit length. By considering Cayley-Menger determinants, this simplex can indeed be realised. You can draw the graph showing which edges are long and extra-long, and observe that it is not vertex-transitive.
The dimension can be reduced to 5, with a 6 point counter-example. Use basically the same trick with the near-regular simplex ABCDEF with AB = BC = CD = DE = EF = FA = 1.000001 and AC = BE = DF = 1.000002 and all other lengths equal to 1. Every vertex has a 1.000002 edge, two 1.000001 edges and two 1 edges, but there is no automorphism taking A to B.
Pingback: Betts revisited | Complex Projective 4-Space
Pingback: Space variant of problem 5 from RMM 2011 | Question and Answer