As a brief summary, I posted about the three-dimensional generalisation of a particular two-dimensional problem by Alexander Betts. In case you haven’t read it, or didn’t understand it, I’ll explain the ideas again here.
A finite set S of n points in d-dimensional space R^d is Bettsian if, for every point X in S, the set of distances to the remaining n−1 points is the same regardless of the choice of X. Here’s a concrete example in two dimensions, namely the vertices of this rectangle:
The distances from each point to the other three are {3, 4, 5} (the last being the diagonal length), irrespective of which vertex you choose. This example also has the property of being vertex-transitive, i.e. we can rotate and/or reflect the rectangle to move any specified vertex to any other specified vertex whilst preserving the shape. Informally, this means that ‘all vertices are identical’.
All vertex-transitive sets are necessarily Bettsian, but does the converse also hold? In one dimension, it’s pretty trivial to see that the only examples have one or two points (consider the distance between the leftmost and rightmost point). In two dimensions, it’s less easy to see that all Bettsian sets must be vertex-transitive, but again it is true (as a corollary of the original question from the 2011 Romanian Masters of Mathematics competition).
A natural question to ask is whether this holds in all dimensions. After my original post, James Cranch provided a 15-dimensional counter-example. With similar principles, it’s possible to reduce the number of dimensions to six. Ben Elliott and I quickly found this particular example:
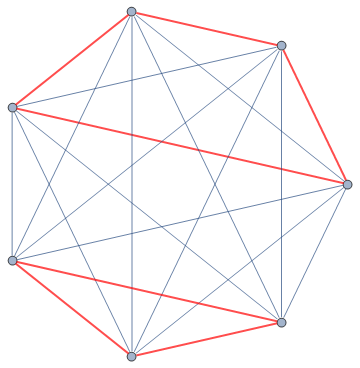
We embed this graph K7 into 6-dimensional space, ensuring that the blue edges are length 1 and the red edges are some other length (1.001 should suffice). There is enough ‘room’ for us to be able to prescribe any combination of edge lengths, as long as they are sufficiently close together (imagine a wire tetrahedron in three-dimensional space). It is clear from the graph that this corresponds to a Bettsian set which is not vertex-transitive.
The same proof does not immediately work in five dimensions, since we can’t colour K6 with two colours to result in a Bettsian graph which is not vertex-transitive. Fortunately, using more colours actually works. Three is actually sufficient, as demonstrated by the following graph:
So, letting the green edges be 1.001, the purple edges be 1.002 and the rest be unit length, we have a five-dimensional non-vertex-transitive Bettsian set. This colouring approach fails spectacularly for smaller complete graphs, and we can conclude that the smallest non-vertex-transitive Bettsian sets have at least six vertices.
Much harder in R^4 and R^3
Reducing the number of dimensions then becomes much trickier. The edge lengths are no longer reasonably independent, so we can’t just choose values arbitrarily. We want to have as much freedom as possible, so we’ll give the previous graph five colours instead of three:
If we set blue edges to have length 20, green edges to have length 18, yellow edges to have length 16, red edges to have length 14, and purple edges to have length 12.6815188243… (actually the root of a horrible polynomial involving an unsolvable quintic!), then the entire thing collapses down into four dimensions. Moreover, this is actually consistent, as we don’t break any triangle inequalities, tetrahedral inequalities etc. More than being merely vertex-intransitive, we have no symmetries whatsoever!
This problem is so hard in three dimensions that we haven’t solved it*. This tends to be a common theme in mathematics: two and fewer dimensions are too trivial, whereas high dimensions enable crazy constructions. It seems to be the case that three dimensions is always the last case to be solved (c.f. Poincare conjecture), with R^4 not far behind.
* We found that up to similarity we have precisely one degree of freedom for the 5-colour K6. There is also a one-parameter family of vertex-transitive solutions of this form, where three colours are identical and the shape is a twisted prism. Regular octahedra mark ‘crossroads’ where these one-parameter families of twisted prisms meet. It’s entirely possible that, just like R^2, all Bettsian sets in R^3 are vertex-transitive. If so, we can fully characterise them.




Pingback: Outer automorphism of S6 | Complex Projective 4-Space
Is there a lower bound for the minimum number of vertices in a non-vertex transitive bettsian set of points in R^3?
Yes, 6 vertices.
So, there still isn’t a proof that no matter what lengths you choose for the Elliot configuration, it won’t collapse into three dimensions?
Correct. The parameter space is five-dimensional, which can be reduced to four-dimensional if you `projectivise’ by identifying scalar multiples (or by setting one side-length to 1). Adding a slider to smoothly vary the second side-length, it should be possible to give a surface plot of solutions with no 5-volume, and those with no 4-volume will appear as singular points on the surface.
Update: I’ve tried messing around with FindRoot[], and only obtained the trivial `twisted prism’ solutions to the 3D Elliott configuration equations. Of course, this doesn’t preclude the possibility of a difficult-to-locate root.
I suspect that Bettsian vertex-transitive in three dimensions, as it is highly unlikely that a more complicated graph than the Elliott configuration would collapse into three dimensions. So, how would we go about proving this? Obviously, all of the vertices must lie on the (wlog unit) sphere, so it is equivalent to the analogous problem in two-dimensional spherical geometry.
Also, note that if we have a solution without central symmetry, then we can double the number of vertices to obtain a solution with central symmetry (and we should be able to eliminate non-vertex-transitive solids which `double’ to form vertex-transitive solids, as we have a complete classification of the latter). Hence, it suffices to consider solutions consisting of pairs of antipodal points (i.e. lines through the origin).