The sinc function is important in signal processing for removing noise and reconstructing the original signal. It’s defined rather simply as sin(x)/x, so it’s surprising that it actually has its own special name (you have to be careful at x = 0, but the limit is sensibly defined as 1). As you can see in the formula and depiction below, sinc is an even function:
The integral under the curve evaluates to π:
A couple of people called Borwein noticed that this identity generalises:
However, this breaks down once you get as far as the term containing sinc(x/15), at which point the integral evaluates to some horrible rational multiple of π instead!
For a more impressive variation on this theme, replace the odd integers with non-composite numbers congruent to 1 (mod 4), i.e. 1 and primes of the form 4k + 1. The pattern continues up until the following point:
Once you add the next term in this sequence, 493541, the pattern breaks down spectacularly; the resulting value is only an inconceivably microscopic distance from π.
The Polya conjecture
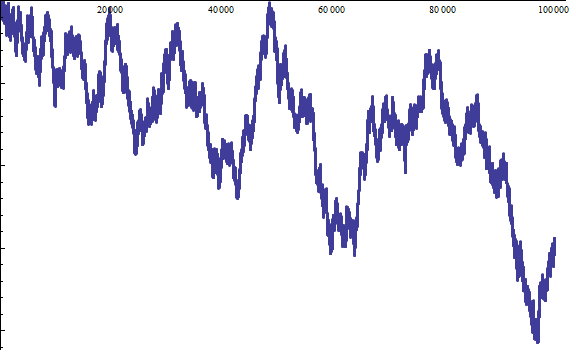
George Pólya conjectured that, for every N > 1, the proportion of numbers n ≤ N with an odd number of prime factors (including multiplicity) is at least ½. This is what the situation looks like for the first few positive integers (N up to 100000). If the blue line hits the horizontal axis, the conjecture breaks down:
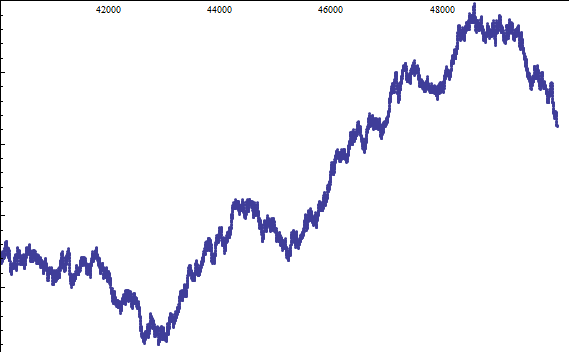
There seems to be some anomaly around N = 50000, where it is dangerously close to the horizontal axis. Fortunately, the zoom below demonstrates that there exists a hair’s breadth between them, so we’re safe … for now.
Indeed, we’re actually safe for quite some time. We can go well into the hundreds of millions before encountering a difficulty. However, in the spirit of Murphy’s Law, we do eventually find a counter-example. The first proof demonstrated that there’s a counter-example somewhere around N = 10^361. Since then, exhaustive searches confirm that the first counter-example is N = 906150257 (which looks prime, but isn’t; it has a pair of 5-digit prime factors).
Skewes’ number
Since the time of Euler, it was known that approximately N/log(N) of the numbers below N are prime. Legendre refined this estimate to N/(log(N) − B), where B is a number called Legendre’s constant. It was first estimated to be about 1.08366, but has since been shown to be precisely 1!
A further refinement by Gauss gives the number of primes below N as the value of the following integral, called the logarithmic integral:
Li(N) was conjectured to always be an underestimate of the number of primes below N. It transpires that eventually this breaks down. An initial upper bound for the first time at which this occurs is Skewes’ number, roughly e^e^e^e^e^e. We now know that the conjecture breaks down somewhere between 10^14 and 10^317.
Stupidly large integers
To quickly conclude, there are many questions in combinatorics (Ramsey theory, for instance), where even the lower bounds are mind-bogglingly massive. Harvey Friedman defines n(k) to be the length of the longest possible sequence {a_i} over a k-letter alphabet such that no block of letters {a_i, a_(i+1), …, a_2i} occurs as a subsequence of a later block {a_j, a_(j+1), …, a_2j}.
We have n(1) = 3, n(2) = 11, n(3) > A(7000) (where A is the Ackermann function) and n(4) > A(A(… A(1) …)), where there are A(187196) compositions of the Ackermann function. To put this in perspective, it dwarfs Graham’s number. Later terms are incredibly, overwhelmingly large.
Friedman then defined a function TREE, which grows so large that even TREE(3) is massively immense compared with n(4). I’ll discuss this later.

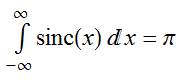
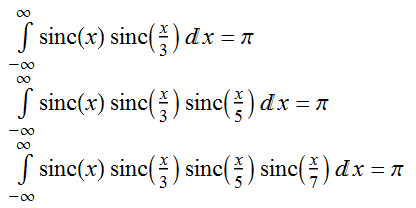
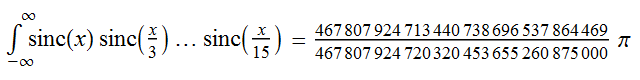
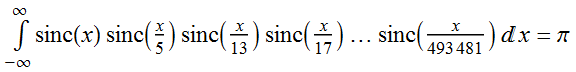
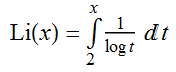
Nelson, a (perhaps kooky?) mathematician at Princeton wrote a paper called “Warning Signs of a Possible Collapse of Contemporary Mathematics”: https://web.math.princeton.edu/~nelson/papers/warn.pdf
where (if I understand correctly) he claims that there’s a difference between multiplication and exponentiation, and that it is moderately reasonable to believe that multiplication is total, but that exponentiation is not total – or at least not provably total.
Harvey Friedman wrote a paper called “Demonstrably Necessary Uses of Abstraction”: http://www.math.osu.edu/~friedman.8/pdf/RADEM092602.pdf
If I understand correctly, he says that the proofs of totality of the various very-fast-growing functions that you mention require gradually stronger inductive principles. So you could work in a logic weaker than the one necessary to prove Friedman’s n function total, or strong enough to prove n total, but not strong enough to prove TREE total.
Is that a reasonable gloss? I’m only a dilettante, and I certainly do not understand the arguments in detail.
Fast-growing functions can be associated with countable ordinals:
In the environment of first-order Peano arithmetic, you can’t do transfinite induction beyond epsilon_0 (which is much smaller than the small Veblen ordinal). Hence, it’s impossible to prove that the TREE function is total just using first-order Peano arithmetic.
This is an awesome post! I wonder if I can http://xkcd.com/217/ someone with the sinc identities…
Quite possibly. If you have a modern calculator which does ‘exact’ arithmetic, you can fool it by entering “ln(640320^3+744)/sqrt(163)” and watch as it gives pi as the supposed ‘answer’. This demonstrates that it must use inverse symbolic lookup, similar to (but not as sophisticated as) Robert Munafo’s RIES.
Pingback: Infinite monkey theorem | Complex Projective 4-Space
プラダ 財布 メンズ 男 カバン http://www.bagsoinsist.info/