It is widely acknowledged that an infinite number of monkeys sitting at computers typing randomly will almost surely produce a properly-LaTeXed copy of the complete works of Shakespeare. This statement, known as the ‘infinite monkey theorem’, has received a wide amount of coverage in popular culture.
Indeed, researchers actually experimented to see what would happen in reality with a finite number of monkeys. The theorem failed spectacularly, with the monkeys vandalising the typewriter, bombarding it with miscellaneous excreta, and typing mainly the letter ‘S’.
Deterministic variant
An alternative of this is where a machine is programmed to deterministically produce all possible outputs. For instance, if we want the machine to eventually produce all English words, one possible solution is to produce all 26 one-letter strings, followed by all 26² two-letter strings (in lexicographical order), then all 26³ three-letter strings, and so on ad infinitum. There was a very poor proposed question on the IMO, which asked for the Nth term of this sequence, where N was some arbitrary integer (somewhere between 10^10 and 10^20, I believe).
There is a formula, known as Tupper’s formula, which defines a subset of the set Z^2 of possible ordered pairs of integers (x,y). If you plot this subset on the plane, and look in the appropriate position, you’ll see a pixellated version of Tupper’s formula itself.
Essentially, this converts floor(y/17) into binary, partitions it into blocks of length 17, and writes them vertically from left to right. If you choose an appropriate (pretty large!) value of y, you can get any binary image of height 17 pixels. This includes the complete works of Shakespeare rendered as a long unbroken line.
Self-referential GoL pattern
Several years ago, I created a machine in Conway’s Game of Life which sequentially prints every possible binary image in a slowly-expanding octant of the plane. Unlike Tupper’s formula, the dimensions of the images are not limited. So, as time progresses, you’ll see gigapixel images of the Mona Lisa and huge renderings of the Mandelbrot set. Eventually, it would even show a picture of its own initial configuration, very much in the style of Tupper’s formula.
Its diameter grows at the slowest asymptotic rate possible, namely Θ(sqrt(log(t))). If the diameter of a pattern has a slower asymptotic growth rate, it would necessarily repeat the same state twice and settle into an infinite loop (thus stop growing). For cellular automata on a hyperbolic plane, this growth rate can theoretically be reduced to the impressively slow Θ(log(log(t))). Coincidentally, this is the same growth rate as the prime harmonic series:
I exploited this slow growth rate to design the sequence of Borwein integrals which fail after the 20479th term.


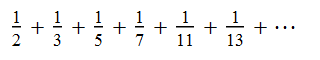
Did you publish that GoL pattern somewhere?
It was on the Internet, but I think that site went down. I’ll e-mail you a copy of it, if you’re interested and have Golly.
I’m interested and I do have Golly. 🙂
I’ve sent a copy of the pattern to you and Wojowu. The reason I can’t upload it to cp4space is that it’s a .mc file, and WordPress only allows certain predetermined file extensions.
May I also have a copy of this pattern? Maybe you could upload it somewhere. How large is the file?
The usual workaround for such issues is to put the file into a ZIP archive. In almost all applications ZIP files are among the accepted upload file formats.
I don’t belive that you made such pattern in GoL, because of orphans. Unless your pattern used another technique, like block-next-to-block (I mean 2×2 block still life)
It didn’t use individual cells as pixels (that would indeed be impossible for precisely the reasons you stated). Instead, it used well-separated boats as pixels.
I’d like to see that pattern too 🙂 As a replacement, I created in Golly 9-state rule table which also creates every possible 2D pattern (finite ones only). Within first 100 mln maximal cell count was 51, and it could be half of that without frame I needed for my design.
Do you still have that GoL pattern? I’d love to see it 🙂