At the tenth Gathering for Gardner, Colin Wright proposed the following problem. It’s quite well known, and I believe it has been published elsewhere before:
‘Dissect a [unit] disk into congruent parts at least one of which avoids the center by a positive distance’.
Bill Gosper posted this to the math-fun mailing list, where it attracted quite a lot of attention. Several people subsequently solved it, including Neil (Bickford?) and Jessica (Kleber?). It is by no means obvious that such a solution should exist, although the pieces must satisfy certain properties, such as having both convex and concave circular arcs of equal curvature to the unit disc. Invariably the first solution that people encounter is this one:
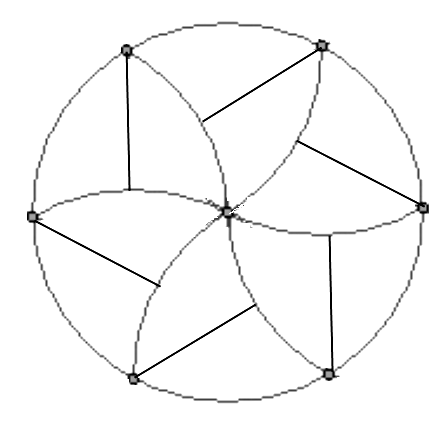
After a little additional thought, other solutions present themselves, such as the one below:
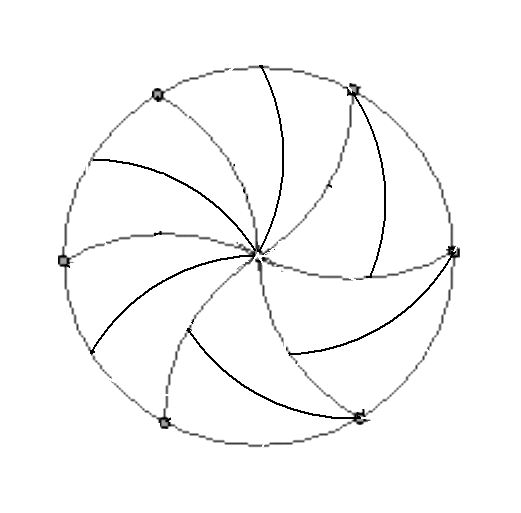
Both of these solutions use curvilinear triangles as the basic unit. It’s possible to fully characterise and enumerate all possible solutions involving curvilinear triangles. The proof is a messy geometrical case-bash, which involves showing that:
- The only possible combinations of edges are {convex, convex, concave} and {convex, flat, concave}.
- The length of each curved edge is strictly less than π.
- The interior angles sum to strictly greater than π.
- For the solution with three curved edges, two of the edges must be of equal length (isosceles curvilinear triangle). From there, one can deduce that this length is equal to 1 (consider both areas and the difference between the convex and concave arc lengths). The smallest concave edge must be a divisor of the length of the largest concave edge, whence we get that there are 6n pieces.
- For the solution with two curved edges and one straight edge, the angle opposite the convex edge is a right angle. It transpires that no solution exists other than the symmetrical dissection into 12 pieces.
Using Burnside’s lemma (MODA, chapter 1) and a boring combinatorial case-bash, these solutions can be exhaustively enumerated. Treating congruent solutions as being the same, the number of solutions for 6n pieces is given by {0, 31, 57, 99, 158, …} (A193362) (the exceptional case where the pieces have a flat edge is included in the number 31).


First of all, let me say that I am amazed by this blog- not just in the rapidity of the posts, but also in the quality of each one.
However, I’d just like to note that in no way was I one of the first solvers- in fact, I suspect (though am not sure of) that it had been circulating around for a while before it was posted to math-fun, and that it was possibly even mentioned at G4G9! Colin Wright, in his series of four posts on it and related problems (the first of which is at http://www.solipsys.co.uk/new/DissectingASquare.html?ColinsBlog ) says he first heard of it “mid-2009”, which means that many others probably solved it even before he popularized it (?).
Additionally, http://mathoverflow.net/questions/17313/is-it-possible-to-dissect-a-disk-into-congruent-pieces-so-that-a-neighborhood-of (ca. 2010, just before G4G9) claims that the puzzle is listed as an open problem at the bottom of page 87 of Croft, Falkoner, and Guy’s “Unsolved Problems in Geometry”, ca. 1991 ! (I don’t have a copy of the book to verify this)
In any case, I don’t deserve any credit for solving the problem.
–Neil Bickford
Looking down at my T-shirt, which contains a solution to this problem (second left from bottom row, for what it’s worth) and well predates 2009, I am appalled that anyone would think that this is actually so recent!
Just kidding 🙂 (Though the T-shirt part is true – I do have a T-shirt with a solution, and it predates 2009. Long story.)
Actually, this puzzle was Problem 4 for 8th grade (“Level A”, apparently, in the English-language book) at the 68th Moscow Mathematical Olympiad (in 2005), so it is definitely at least that old; it is simple enough that I suspect it is probably significantly older (I won’t be surprised if it appears in a Steinhaus book).
EDIT: Apparently, the “exceptional” solution is the logo for Mathematics Advanced Study Semesters, of Penn State, attested with explanation back to 1999; again, the context seems to suggest that the puzzle itself is relatively well-known and older. I still stand by my conjecture that it dates back at least to Steinhaus (and of course it could well be even older).
Update: Did I say back to 1999? Make that back to January 1997:
https://web.archive.org/web/19970124054553/http://www.math.psu.edu/mass/