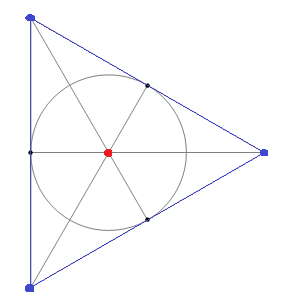
The Encyclopedia of Triangle Centres contains a collection of over 5000 different points in the plane of a triangle, represented by the letter X followed by an identifier. The well-known triangle centres include the circumcentre (X3), centroid (X2), orthocentre (X4) and incentre (X1), which are all too familiar to anyone who has studied Euclidean geometry. A few other common centres and the relationships between them are featured in this image from MODA:
There are more obscure ones such as X115, which is defined as the intersection of the asymptotes of the unique hyperbola passing through the three triangle vertices, the orthocentre and the centroid! This is known as the Kiepert hyperbola, which is a rectangular hyperbola containing many interesting points. Indeed, any hyperbola passing through three vertices also passes through their orthocentre if and only if the hyperbola is rectangular.
One of the latest triangle centres to be added, X5396, is even more obscure — it’s the intersection of the line joining the incentre to the nine-point centre and the line joining the circumcentre to the symmedian point.
There is even a Java applet to allow you to explore the triangle centres {X1, X2, …, X1000}. With so many triangle centres, you get loads of concurrencies, collinearities and concyclicities. One can also find cubics containing lots of interesting points; an example is the Neuberg cubic, which appears to pass through the three vertices, four centres of tritangential circles, the circumcentre, and a plethora of triangle centres:

A topologist, James Cranch, proposed a geometry where every triangle has just one centre: ‘the point in the middle of it’. Even though this may seem imprecise, definitions like these are perfectly acceptable from a topological perspective, as all points inside a triangle are pretty much equivalent. (Indeed, this is what James Cranch looks like to other topologists:)
His suggestion was not intended to be taken seriously, although the notion does lead to interesting concepts. One such ‘Cranch geometry’ is obtained from the Fano plane, where we map each triangle to the unique point which doesn’t lie on any of its three sides:
The ‘Cranch centre’ of the blue triangle is indicated in red. Note that if D is the Cranch centre of triangle ABC, then A is the Cranch centre of triangle BCD. This symmetry property also applies to the orthocentre in Euclidean geometry, but this isn’t a Cranch geometry as the orthocentre can lie on one of the sides of the triangle.
After taking the symmetry property as an additional axiom in the definition of a Cranch geometry, it is interesting to consider which projective planes satisfy these axioms. By counting the number of triangles in a plane with N² + N + 1 points and noting that it must be divisible by 4, it can be inferred that N is either even or of the form 8k − 1 for some positive integer k. Also, it’s not too difficult to show that all projective planes of infinite order admit Cranch geometries, provided we assume the axiom of choice.
For projective planes over finite fields, the property that ‘any four non-collinear points can be mapped to any other four non-collinear points’ means that there isn’t a unique Cranch geometry for any such plane other than the Fano plane. However, we don’t yet know whether there are Cranch geometries over the plane with 57 points (there are either none or lots).


Is James really equivalent to a sphere with 6 holes? I thought he just had three.