Some things have actually happened. A few of these are worth mentioning.
RMM 2013 results
Firstly, the results of the Romanian Master of Mathematics (RMM 2013) competition have been published. There have been two perfect scores this year (very rare for RMM), namely Ömer Cerrahoğlu (Romania) and Krachun Dmitrii (Russia). Third in line was our very own Matei Mandache, who scored an impressive 35/42, achieving a gold medal in the process. The UK team also had another gold medallist, namely Daniel Hu.
The UK team came third (beaten only by the USA and Russia), achieving two gold medals, a silver and a bronze. The two remaining contestants each had a Double Honourable Mention, which is very respectable for competitions of this difficulty.
Multicoloured ants
Tim Hutton, Ed Pegg, Georgi Gochev and Mark Jeronimus have been exploring the space of generalisation of Langton’s ant. The threshold for non-trivial examples to appear is 1 state and 2 colours; Langton’s ant lies on this boundary, as does a modification emulating binary counting.
The latest discoveries in this area include multicoloured ants that emulate Langton’s ant, but taking increasingly long amounts of time to do so. This is no longer a mystery, and can be explained by the reversibility of the original Langton’s ant. The proof of the Cohen-Kung theorem extends to show that these generalisations also settle into building a periodic highway.
For 1-state 3-colour, the 3-colour Langton Ant is beaten by a turmite that also emulates Langton’s ant, but in a very different way. Specifically, it alternates direction between forwards and backwards, and takes 18.5 million generations (as opposed to 2.67 million) before settling into a cycle of gradually increasing length. Its asymptotic growth rate is , where t is the elapsed time.
Both of these are beaten by a completely different 1-state 3-colour turmite, which takes 67 million generations to settle into a periodic highway. Here you can see the mess left behind by the turmite before escaping to the left:
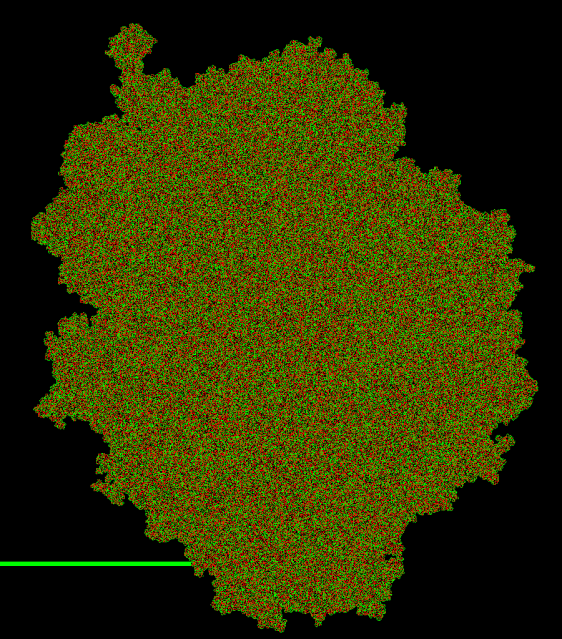
There are 9 unresolved Turmites in this space, so it is possible that there are even longer periods of time before stabilisation occurs. These have all been explored for at least 10 billion generations, and show no signs of becoming predictable. One of these exhibits binary counting behaviour:

When the amphisbaenic binary counter reaches the mess to the right, it is expected to become unpredictable again. It is unknown whether, at any time, one of these binary counters is created in a position where it would expand forever. I conjecture that this turmite does eventually become predictable. Firstly, by the Law of Excluded Middle, precisely one of the following must necessarily apply:
- The turmite is unbounded, and therefore the bounding rectangle must continually expand. This can only happen if the turmite touches the perimeter of the bounding rectangle infinitely often. Every time this occurs, there is a nonzero probability of producing a binary counter in such a position where it expands forever.
- The turmite is bounded in a N by M box, in which case it can last for at most
generations before entering a periodic cycle.
Of course, this is not guaranteed to happen, since the turmite could continually evade placing binary counters at the perimeter (similar to tossing an infinite sequence of heads on a fair coin). Alternatively, it may ultimately enter some other type of non-chaotic behaviour, such as constructing a highway (in which case it is still predictable, and therefore still satisfies my conjecture).
For 2 states and 2 colours (the subject of Ed Pegg’s turmite challenge), I mentioned how Worm Trails had been beaten twice, with the current champion lasting 240 million steps. This record has been smashed another two times. Firstly, Gochev provided one with a lifespan of 7.735 billion steps, which finishes by constructing an expanding triangular wedge:

Georgi then broke his own record rather spectacularly, giving an example with a lifespan of 3.511 trillion generations. This one eventually produces an infinite highway:
Amonst the unresolved 2-state 2-colour turmites, a few produce interesting patterns:
This one produces ephemeral orthogonal and diagonal highways in its interior:




I wonder what’s the definition of ‘becoming predictable’. Strictly speaking, as long as we can simulate it, each of its steps is predictable as we can figure exactly how it will look like in Nth generation as long as we can simulate it to N. If we assume that we can build a simple formula telling us how it will look in Nth generation without simulating it all N steps, I wonder if e.g. an ant which was building a ladder of pseudorandom numbers was considered predictable or not. Or a bifurcation diagram?