Consider the Gaussian function . This gives the standard normal distribution, which has zero mean, unit variance, and points of inflection located at ±1. Note the scaling term
, which is included so that the integral is 1 (necessary for a probability distribution). Specifically, we have:
This is not so surprising, and can readily be derived from considering a two-dimensional Gaussian distribution. Much more unusual is that this related function also has an integral of √(2π) (although suitable changes of variables should relate these integrals).
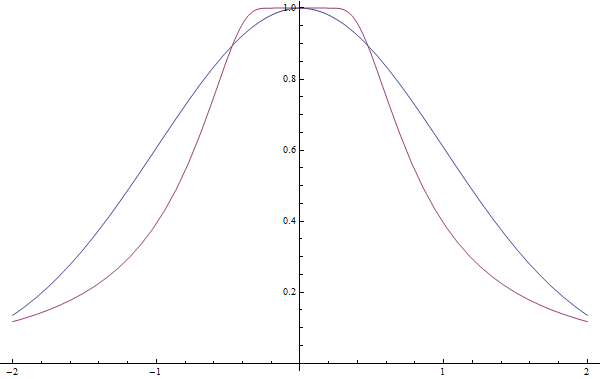
This function is much more bizarre than the normal distribution. Firstly, it is completely flat (i.e. all derivatives are zero) at its peak:
Intriguingly, it is only completely flat at a single point (unlike, say, a horizontal line segment, which is completely flat on an interval). It is quite strange for an infinitely-differentiable function to have this property, and completely impossible over the complex numbers. If we look at what happens near zero, you’ll notice some stunningly pathological behaviour:
Anyway, I digress. What I actually wanted to talk about was the ubiquity of √(2π). It also occurs in the definitions of the continuous Fourier transform and its inverse:
You may have heard the amusing arguments debating whether it’s better to use π or τ = 2π as a fundamental constant. We have had a Tau Manifesto, which was soon met with criticism in the form of the Pi Manifesto. I propose a third competing faction, namely Radical Tauism (it’s funny because ‘radical’ can mean ‘(square-)root’ as well as ‘extremism’ ;P), which insists that √(2π) is better than the other two alternatives. In order to win, I suppose I’ll systematically deconstruct the arguments of the opposition parties.

Shown above is an image from the Pi Manifesto. It shows a unit circle, which has equal area to a square whose diagonal length is … erm … √(2π). Oh, yes, I forgot to mention yet another occurrence of √(2π), namely Stirling’s asymptotic formula for the factorial function.
The main benefit, however, is that both pi and tau can be expressed as polynomials in √(2π), whereas the converse is false. Square roots are ugly (being multi-valued when extended to the complex plane), so it’s cleaner and more elegant to eliminate them completely by inventing a new symbol for √(2π). The question is, which symbol? We want something relatively simple, which excludes (for example) the Chinese ‘biang’ character:

I look forward to seeing your comments and criticisms.

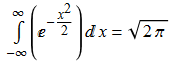
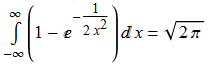
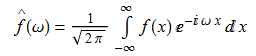
I’d propose this character: 厩
It’s definitely simpler than biang…
😉
Indeed it is. Apparently, there’s an even more complicated Chinese character, which loosely translates as ‘the image of a dragon in flight’.
It’s actually a Japanese Kanji. The one you’re looking for is http://en.wikipedia.org/wiki/Taito_(kanji).
Thanks!
I propose: √(2π) …. treated as a single symbol. (similar to the connection of “e” and “t” to “&”)
I think we should register a unicode number for that symbol, and integrate (pun intended) it into all common character sets.
I don’t have any thoughts on the pi, tau or radical tau issue, I just wanted to comment on your digression. I have often wondered if an infinitely-differentiable function could be completely flat over some domain, specifically I’d wondered about a function which was constant over some domain and could then become non-constant outside of that domain. I’d always assumed (without any analysis) that some derivative would have to be step-wise continuous at the edge of the constant domain. This might still be true for all I know but I was still amazed by your example here of a function which is completely flat at some point.
While I’m here, I’d like to say that I have really enjoyed your blog over the last few months. I come to this with a university physics background and a fascination of pure maths but have moved on since then and don’t often work through problems. However, your ciphers do intrigue me and I had a decent crack at “The scenic route”. I loved the pun and tried to come up with several potential solutions – but to be honest I still wasn’t sure how many turns on the path encoded each letter. I hope you don’t mind me commenting on one of the ciphers – but I don’t think I’ve revealed anything other than my ignorance of cryptanalysis.
Pingback: Gamma(1/4) | Complex Projective 4-Space