This is the first of a projected series of articles investigating a natural three-dimensional generalisation of chess. In the first article, I’ll briefly describe the rules and mention previous research in this area. The second article will show how to create a linear-bounded automaton (the construction also being applicable to two-dimensional chess). The third and final article will extend this to a 3-counter machine comprising finitely many pieces on a board, thereby proving that three-dimensional chess is Turing complete with finitely many pieces. The analogous problem in two dimensions is still unsolved, and I believe this to be the first proof for three dimensions.
The pieces
The pieces are the same as in original chess, but modified to operate on the three-dimensional cubic lattice instead of its two-dimensional counterpart.
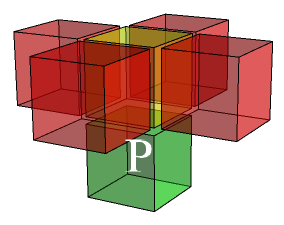
A pawn can move forward a single space, or capture diagonally in any of four directions. White pawns move upwards (increasing z coordinate), whereas black pawns move downwards (decreasing z coordinate). Theoretically, a pawn can move two spaces on its first move, and the en passant rule still applies; however, this does not affect the Turing-completeness proof (which is what we’re interested in).
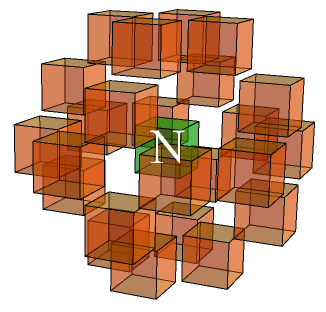
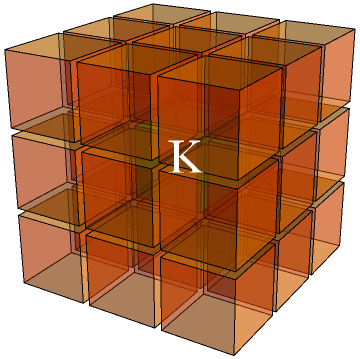
A knight can move to one of any of the 24 spaces at a distance of precisely from its current position. The parity of a knight’s position alternates each time it is moved.
A rook can move to any space that differs from its current position in a single coordinate, assuming that the intervening spaces are all empty. This is the simplest piece that has a potentially infinite set of moves on a single turn.
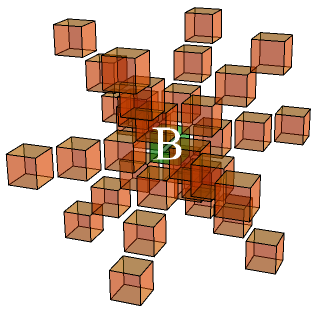
The bishop can move in any of twelve directions. I had a dilemma about whether to define the bishop to move diagonally (as above) or triagonally. I chose the former because, as with the ordinary bishop from two-dimensional chess, it is confined to squares of a single parity. This is consistent with the bishop in the existing three-dimensional chess variant of Raumschach; however, our pawns differ.
The king can move to any of the 26 squares at a unit Chebyshev distance. Unlike ordinary chess, there is no bound on the number of kings a player can have. The game terminates as soon as one player captures an enemy king. This is a much simpler definition than the ordinary checkmate condition, and almost equivalent (the exception is stalemate, but this never occurs in the Turing-completeness proof).
In the game of Raumschach, there are two additional pieces: the unicorn (which moves triagonally) and the queen (which combines the moves of a rook, bishop and unicorn). I don’t require either of these pieces in the proof of Turing completeness, and may even be able to dispose of the bishop.
The next article will include constructions of logic gates using these pieces.


In the question about 2D chess Turing completeness, are we forced to use standard chess rules, or can we, for example, use fairy chess pieces?
Standard chess rules, ideally. Generalised chess pieces would render the problem vastly easier.
Pingback: Circuitry in 3D chess | Complex Projective 4-Space
Pingback: 3D chess is Turing-complete | Complex Projective 4-Space
Pingback: Getting Fancy: Special Chess Moves | Games
Cool, but I disagree with the bishops and knights only retaining 2d movements. If the queen and king can move in all 26 directions, it makes no sense that a queen could attack a bishop but the bishop wouldn’t be attacking back. Also, triagonal bishops would still only be able to access half the cubes on the board if 2d moves are excluded, a 3d bishop could only move to the cubes whose coordinates sum to the same even/odd-ness of the number. Colors would alternate along 3d diagonals. The knight should also be able to make a diagonal move perpendicular to its initial 2 cube movement, as the definition of a knights move is to any cube that’s not on the same file, rank, or diagonal. So it actually has 48 possible moves! The rook is actually the weakest piece in cubic chess! The pawn should also be able to capture upward diagonally, like an upward-shifted king move. All pieces should retain both 2d and triagonal type moves for consistency in my opinion.
Edit: Knights move is to the closest cube not on the same straight line in any direction, including triagonals, so that allows slanted L shapes.