In 2010, Evangelos Kranakis and Danny Krizanc published an academic paper with a rather bizarre title. The Urinal Problem investigates a particular mathematical model arising from the behaviour of men selecting urinals in a bathroom arrangement. Rather atypical of mathematical publications, one of the figures is a full-colour photograph of a line of urinals:

Figure 1 of The Urinal Problem
One particular model is where each entrant stands at the unoccupied urinal as distant as possible from the existing people. Randall Munroe added the restriction that no two men may stand adjacent to each other, resulting in a rather light-hearted analysis of the subject. Making the additional assumption that the first entrant stands at one extremum, he derived the ultimate packing density as a function of the number of urinals.
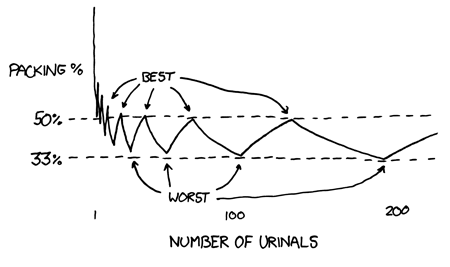
Randall Munroe’s graph of packing density against length
Asymptotically, the best packing density is 1/2, and the worst packing density is 1/3.
Continuous model
I decided to consider what would happen in the alternate environment, where discrete urinals are replaced by a continuous trough (in the Netherlands, there is a specific word to refer to this construct, namely ‘pisbak‘). Assuming without loss of generality that the trough is of unit length, people will stand at an enumeration of the dyadic rationals in increasing order of denominator (and, where two dyadics have equal denominator, the ordering is arbitrary).
Extending this to two dimensions (where the trough is replaced with a field*), the behaviour is more interesting. Here’s an animated GIF I prepared earlier, where the colour of a point indicates the minimum distance to a person:
For a circular field, the problem is much more chaotic, and I don’t believe that there is a nice characterisation of which points are occupied. Indeed, it may be influenced by the arbitrary choices of earlier occupants. In principle, we can generalise further to any metric space.
* No, not a ring where all nonzero elements are invertible. (I realise that if I didn’t include this footnote myself, some of you will have commented…)
Line-of-sight considerations
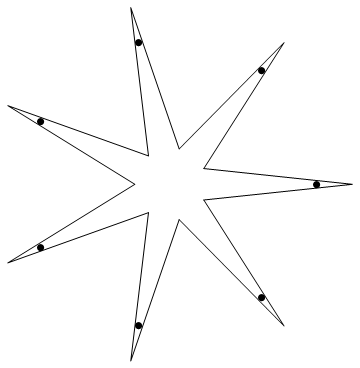
In addition to separation, it is usually desirable not to be making eye contact with fellow occupants. The problem of situating urinals in a bathroom to avoid this resembles a dual of the art gallery problem, which involves placing guards in a polygonal art gallery such that they can view every point. If we want to give n people privacy, it certainly suffices for the room to have 2n edges. For instance, here is a solution to the Privacy Problem for n = 7:
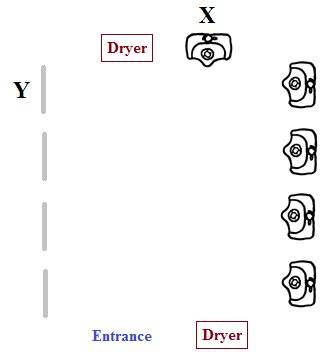
Unfortunately, architects frequently fail to take this into consideration, and actually exacerbate the situation by adding mirrors in bathrooms. For example, Michael Dunn Goekjian (another person with three adjacent unit quaternions in his name, c.f. my IMO report) commented on the poor planning that went into the layout of the bathroom of the Babbage Lecture Theatre, with particular emphasis on the lavatory X orthogonal to the mirror Y:
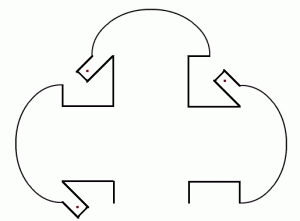
Nevertheless, even if the entirety of the walls are covered with a reflective surface, it is (amazingly) possible to solve the Privacy Problem. Lionel and Roger Penrose realised that the focal properties of an ellipse can be exploited to achieve this:
I believe it is an open problem as to whether a polygonal room can have this property.