Twelve years ago, Kontsevich and Zagier published an enlightening exploration of a set of real (or, more generally, complex) numbers known as periods. Firstly, let’s have a look at which sets are subsets of which other sets:
The integers are a proper subset of the rationals
, which are in turn a subset of the algebraic numbers
(roots of polynomials with integer coefficients, such as
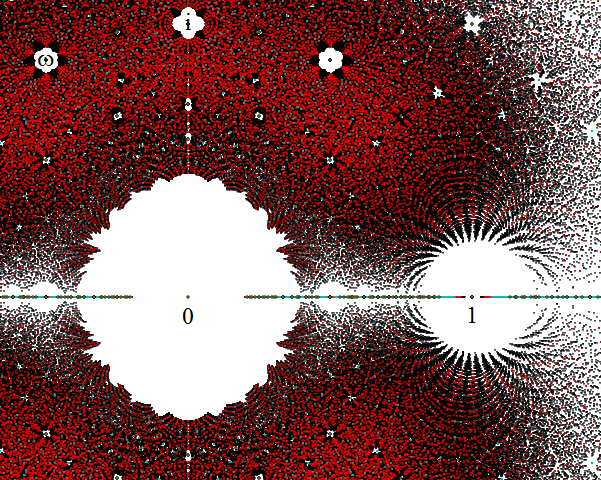
and i/92 amongst other things). The algebraic numbers are a dense subset of the complex plane. Dan Christensen plotted the roots of polynomials of low degree with small coefficients:
Despite being dense in the complex plane, roots of reasonably small polynomials are quite far apart; large holes occur around 0, 1, i and other points, devoid of close algebraic approximations. The real line is also very densely populated, since (for instance) every polynomial of odd degree has at least one real algebraic root.
The field of algebraic numbers is actually quite tame, and we can easily verify whether two algebraic numbers are equal (use Euclid’s algorithm to extract the greatest common divisor of the corresponding polynomials and observe whether or not they share that root). By contrast, this does not apply in the set of computable complex numbers; there is no algorithm for proving that two Turing machines generate the same computable number. We don’t even know whether the Euler-Mascheroni constant γ is rational!
To summarise, algebraic numbers are well understood, whereas computable numbers are deeply mysterious and enigmatic. The algebraic numbers are rather restrictive, excluding important mathematical constants such as π and e. It would be nice to have a larger set of well-understood numbers; this was the motivation for Kontsevich and Zagier’s study.
What is a period?
A number is a period if it can be expressed as an integral of a rational function over a region of determined by polynomial inequalities with rational coefficients (together with Boolean operators). For example, π is a period, since it can be expressed as the integral of 1 over the domain
. Periods are closed under multiplication (take the Cartesian product) and addition (express the integrals as volumes of regions determined by algebraic inequalities, and take the disjoint union of the resulting regions). Hence, the periods form a ring
.
Examples of periods include:
- π (area of a circle);
- Logarithms of algebraic numbers (integrate 1/x from 1 to α);
- Zeta function at integer arguments (including ζ(3), Apery’s constant);
- Elliptic integrals;
- Γ(p/q)^q;
- The lemniscate arc length, S.
The authors of the paper also consider the extended period ring, where 1/π (which is conjecturally not a period) is adjoined to the ring. These rings are equal if and only if 1/π is a period. It is not even known that the periods do not form a field, although this is widely believed to be the case.
All periods are computable (do numerical integration in your favourite computer algebra software running on a Turing machine), so basic uncomputable numbers such as Chaitin’s constant Ω aren’t periods. There is also a just-do-it construction for a computable non-period: start with an enumeration of the periods, and choose your favourite closed interval [a,b]. For each period, select a smaller closed interval (in a computable way) that avoids that period. The intersection of these intervals is a single real number, which is computable but not a period. A more explicit example of a non-period has since been found, analogous to how Liouville constructed a transcendental number.
Identities between periods
In the paper, Zagier and Kontsevich conjectured that two integrals correspond to the same period if and only if they can be related by the following operations:
- Linearity of integrals;
- Changes of variables (such as affine transformations);
- The Fundamental Theorem of Arithmetic and generalisations to higher dimensions.
For example, we can formulate ζ(2) = π²/6 in two completely different ways:
- The integral of 1/(y − x y) over the region 0 < x < y < 1.
- The integral of 1/6 over the four-dimensional region x² + y² < 1; w² + z² < 1.
It transpires that these integrals can indeed be interconverted by use of these three basic operations. If the conjecture is true, we could algorithmically decide whether any two periods are the same: alternate between numerically calculating them (to see whether they are not equal) and trying sequences of basic operations (to see whether they are equal).

Meow
If it walks like an Aaronson, talks like an Aaronson but claims to be a Cranch, it’s an Aaronson.
Correction: If it shuffles along the floor on its back with hands inside its hoodie protruding from its solar plexus whilst using feet for propulsion like an Aaronson…
Don’t blame me! I was peer-pressured into doing it.
Is P-hat the extended period ring, then, or the possibly-still-larger field you get by taking the algebraic closure of P? Said algebraic closure seems like it might be well-behaved and, being a field and algebraically closed, more useful than P itself.
P-hat is the extended period ring, rather than either the field of fractions or the algebraic closure. If you read the paper, I believe P-hat was proposed to include certain values of hypergeometric functions.
Not to be annoying, but the root sets Dan Christensen was studying mostly are not dense; the Littlewood polynomials (the ± polynomials) e.g. cannot have roots smaller than 1/2 nor larger than 2; the picture above seems to be for coefficients not more than 4.
I believe Adam meant that the set of algebraic numbers is dense, so it is a little surprising that sets of roots of ‘small’ polynomials aren’t..