Sam Cappleman-Lynes noticed the seemingly remarkable fact that at least one of the interior angles of a triangle being equal to π/3 is equivalent to the linear relation between the semiperimeter, circumradius and inradius. He provided a clever synthetic solution, and I demonstrated that a mindless algebraic bash (starting from the cosine rule) will also give the same result, where a quartic factor drops out of a sextic to leave a quadratic, which is miraculously the square of a linear term.
This problem made its way onto a sheet of ‘background problems’ at the 2013 Easter Trinity camp. Gabriel Gendler recognised it as being very similar to a theorem he had already seen, namely that a triangle satisfies if and only if it is right-angled. At this point, I conjectured that for every angle
, the existence of at least one angle of θ in the triangle is equivalent to some homogeneous linear equation in (R, r, s).
It transpires that proving even this more general statement is not too difficult, and far more straightforward than any of the solutions presented to the background problem at the Trinity camp. The techniques here are described in MODA, but I’ll assume that you haven’t necessarily read it (or, if you have, remembered it) and include everything here.
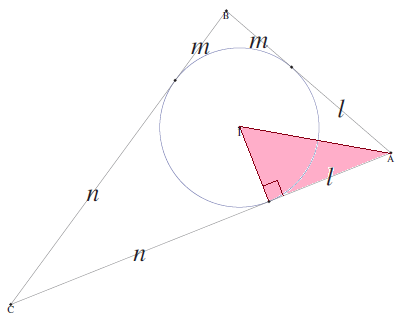
The original solution was so hideously complicated as a result of using the cosine rule. Instead, we’ll use a simpler tangent rule, which facilitates a much shorter proof. If you concentrate on the rose-tinted right-angled triangle in this diagram, you should observe that .
So, the condition that at least one of the angles of the triangle is θ is the following cyclic product, which evaluates to zero if and only if at least one of the factors is zero:
We then expand this as a cubic polynomial in . Each of the resulting elementary symmetric polynomials in (l,m,n) can be converted into polynomials in (R,r,s) using the ‘symmetric polynomial conversion toolkit’, resulting in the following:
After dividing throughout by a factor of r², we obtain a homogeneous linear relationship in (R,r,s) as desired:
Relation to cubic curves
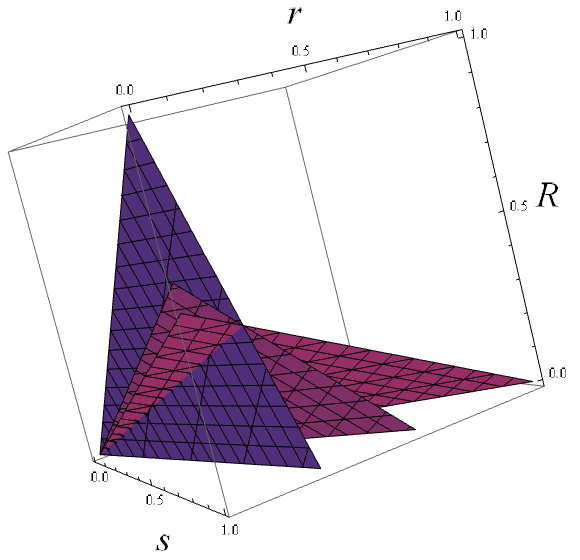
Homogeneous linear equations in three variables correspond to planes through the origin in three-dimensional Euclidean space, . Here, the planes corresponding to angles of 30°, 60° and 90° mutually intersect on a line, representing a set of similar triangles:
However, homogeneity enables us to reduce them to lines on the real projective plane , where points on the projective plane represent different similarity classes of triangles.
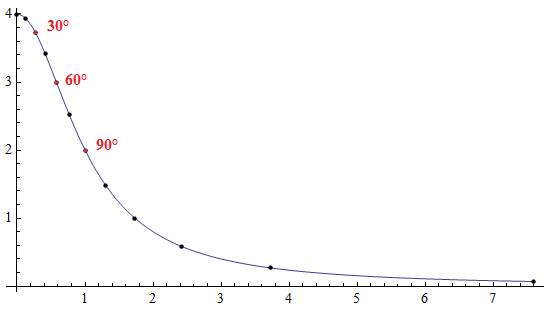
As θ varies, the line on the projective plane moves in a weird way. Using projective duality, however, we can make more sense of this. We now have a point for each value of θ (thus the locus, rather than the envelope, is a curve), and a line passing through that point corresponds to a similarity class of triangles with at least one angle of θ. Isosceles triangles are lines tangent to the curve (therefore doubly intersecting the same point, corresponding to two copies of that angle), and the equilateral triangle is the line tangent to the point of inflection. Our 30°-60°-90° triangle is the line suggested by these three collinear points:
This ‘dual curve’ is actually a cubic, which endows it with a beautiful Abelian group operation by virtue of Cayley-Bacharach (c.f. elliptic curve calculator). In this case, it embodies the fact that the interior angles of a triangle sum to π. I have always said that practically all of Euclidean geometry can be deduced from Cayley-Bacharach, but I didn’t imagine that the geometry of the triangle was so intimately related to elliptic curves.

I just wanted to point out that your equation can be simplified to
\[s = 2R \sin \theta + r \cot (\theta/2).\]
This is the equation presented in “Generalization of a Relation Involving Right Triangles,” by W. J. Blundon, American Mathematical Monthly, Vol. 75, No. 5 (May 1967), pp. 566-568.
Interesting.