In Einstein summation convention, repeated indices are summed over. For example, . If a Kronecker delta has two different suffices, we can ‘contract’ them as follows:
, whereas
.
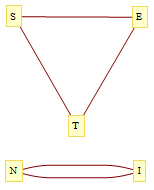
Vishal Patil considered contracting English words in this manner. For example, ‘intestines’ gives us the expression . In general, suppose we have a word W of 2n letters (n pairs of distinct letters in some permutation), and wish to evaluate it in summation convention. Then the product of the deltas evaluates to
, where c is the number of cycles in the n-vertex (multi-)graph produced by joining two vertices with an edge if the corresponding indices share a delta. The graph corresponding to ‘intestines’ is shown below:
English words consisting entirely of repeated letters
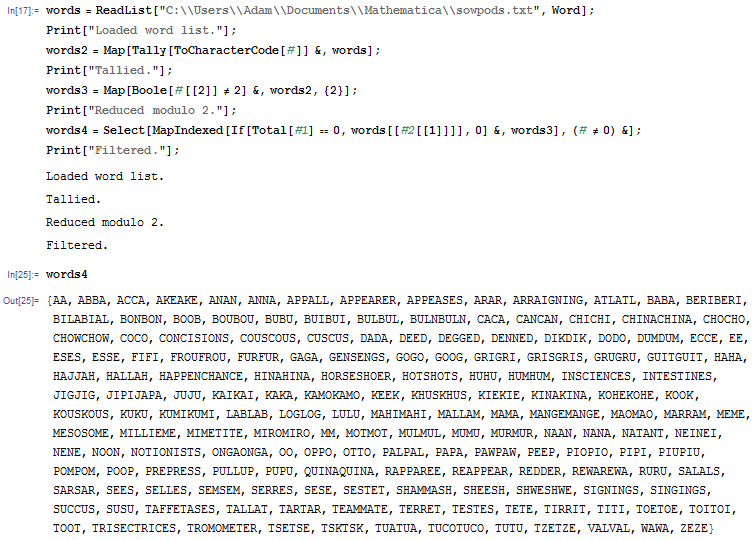
I wanted to find other examples (other than ‘intestines’) of words in the English language which feature each letter precisely twice. To do so, I downloaded the official Scrabble dictionary SOWPODS (verifying that it was comprehensive by checking that it contains the word ‘boustrophedonic’) and wrote the following simple Mathematica program:
As you can see, there are a couple of 12-letter words in there, namely ‘trisectrices’ and ‘happenchance’. Conveniently, 12 is a multiple of 3, so we can evaluate the product of Levi-Civita symbols with these subscripts:
Here I’ve used the fact that the Levi-Civita symbol is invariant under cyclic permutations, and then simplified the expression using epsilon-delta contractions. We can also evaluate ‘trisectrices’:
You can have a go yourself at evaluating expressions corresponding to other English words.
Sum of all words
Suppose we evaluate each of the permutations of aabbcc…dd (with 2n letters) using Kronecker deltas (as we did with intestines) and wish to sum them together. For
, we just have one word with a value of 3. For
, we have six words, two of which have a value of 9 and four of which have a value of 3, so the sum is 30. We can continue this sequence.
If we choose a random word on n letters, the probability generating function for the number of cycles is given below:
Setting s = 3 gives us the expected value of a random word. Multiplying this by the number of words will thus give us the total:
This sequence is already in the OEIS as A007019, but there is no mention of it being equal to the ‘sum of all words’ in Einstein summation convention.

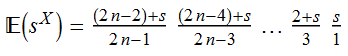

Yes! Finally something about rockstar video games.