The Universe

Some people have recently been discussing Eric Weinstein*, who has proposed a 14-dimensional theory of everything known as Geometric Unity. The media attention is possibly as a result of the trivial difference between his surname and that of the patent office clerk responsible for formulating general relativity.

* Not to be confused with Eric Weisstein, who created Wolfram MathWorld.

Whilst these theories of everything are concerned with the local field equations and particles at the most minute of scales, the large-scale structure of the universe is also very interesting and equally unknown. Here we’ll examine a few suggested candidates for the shape of the universe:

Curvature of space

When you gaze off into the depths of space, it is natural to imagine space as being , an infinite Euclidean space. This is not, however, the only possibility. Space is locally curved (c.f. general relativity), and it has been suggested that it may in fact be globally curved. A constant positive Gaussian curvature would cause the universe to ‘curl up’ into a 3-sphere, whereas a negative Gaussian curvature corresponds to hyperbolic space.

Thanks to Gauss’s Theorem Egregium, it is possible to determine the local curvature by measuring distances in the propinquity of a point. Hence, it is theoretically possible to calculate the radius of the Earth by measuring distances between (four) cities. I tried this and computed a Cayley-Menger determinant; it differed from zero, proving that the Earth is not flat.

Cosmologists have measured the curvature of the universe to be within experimental error of zero, suggesting that (on a large scale) space is Euclidean. If space is indeed everywhere flat, this precludes the possibility of the universe being a 3-sphere. There are, however, several possible shapes, even with this restriction. Conway calls these platycosms.

Platycosms in two and three dimensions

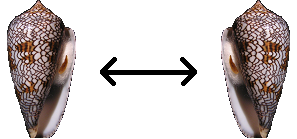
In two dimensions, there are precisely two finite flat manifolds, the torus and Klein bottle. They differ in that one is an orientable surface, whereas the other is not. If we lived on a three-dimensional analogue of a Klein bottle, it would be possible to place a left-handed seashell on a spaceship, send it around the universe, and observe that it returns as a right-handed seashell.

There are ten finite three-dimensional platycosms (mentioned here), which are all feasible candidates for the shape of our universe. Other possibilities include an infinite universe (such as the Cartesian product of a circle and an infinite plane). I’m assuming that the universe doesn’t have a boundary, as this would be really weird.

Poincare dodecahedral space

Certain manifolds can be constructed by taking a simply-connected patch and identifying parts of its boundary. For example, a torus can be produced by identifying opposite edges of the unit square. A more complicated example is obtained by identifying opposite faces of a regular dodecahedron. Depending on how much you twist each face (by 36°, 108° or 180°), you can obtain different spaces (namely a Poincaré homology sphere, the Siefert-Weber space, and , respectively).

Based on data from the WMAP probe, some scientists conjecture that the shape of the universe is a Poincaré homology sphere. The evidence isn’t conclusive, however…