Iterated automorphism groups

This was inspired by a discussion with James Aaronson outside the Chapel. We were contemplating group theory and automorphisms (specifically, trying to determine whether there exists a group of size strictly larger than with only two automorphisms), and eventually considered the following question:

What happens if you begin with a group G, and iteratively apply the ‘automorphism group’ operator?

For a cyclic group of order n, where n has primitive roots, the automorphism group is the cyclic group of order φ(n). If a group is non-Abelian, its automorphism group is also non-Abelian (consider automorphisms arising from conjugation by elements which do not commute). Similarly, if a group is Abelian and non-cyclic, its automorphism group is non-Abelian. Hence, the groups that eventually reduce to the trivial group under repeated application of Aut are cyclic groups of order n such that {n, φ(n), φ(φ(n)), …, 1} all have primitive roots. James Aaronson completely characterised the integers with this property:

• , for all ;
• ;
• Primes p of the form ;
• 2p, where p is a prime of that form;
• 4, 5, 10, 11, 22, 23, 46, 47 and 94.

These form the sequence A117729.

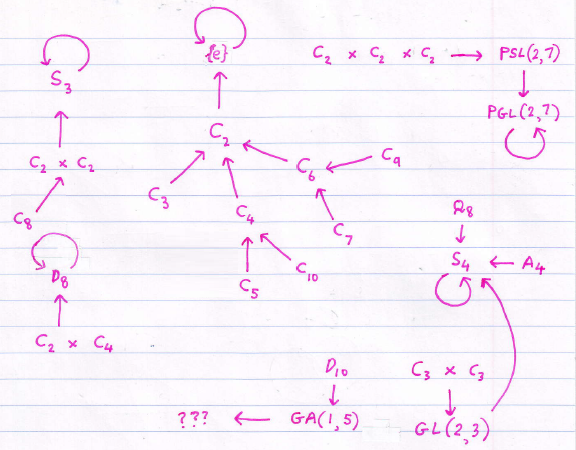
The next case is C8, which has no primitive roots. Its automorphism group is the Klein 4-group, C2 × C2. Since it is the additive group of a vector space over F2, the automorphism group is the group of linear maps (2 × 2 invertible matrices over F2 with linearly independent columns). It is not too hard to show that this is isomorphic to S3 (symmetric group with 6 elements), and that the direct sum  has the general linear group GL(n, p) as its automorphism group.

Most symmetric groups (the exceptions being n = 2 and n = 6) are their own automorphism groups. The next few cases, such as D8 and Q8, are included in the diagram below:

As the size of the group increases, these become difficult to compute.

For simple non-Abelian groups, the automorphism group is complete (equal to its own automorphism group). This is proved here. More generally, for centreless groups, it is possible to define a limit of a sequence of iterated automorphism groups, known as an automorphism tower. It has been proved that this process eventually terminates at some ordinal (not necessarily finite).

This is discussed in further detail on Math Overflow.