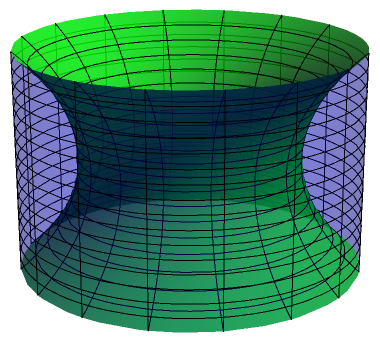
Given two identical circles lying in parallel planes with a common axis of symmetry, what is the minimal surface that connects them? Initially, one might suppose that it is a cylinder (blue in the diagram below).
However, we can quickly establish that a cylinder is not favourable. For a minimal surface, optimal solutions have zero mean curvature, whereas the cylinder has nonzero mean curvature. The correct solution is a catenoid (green), which is the revolute of the curve 
Another minimal surface is the helicoid, obtained by taking the surface swept out by a horizontal line undergoing a continuous screwing about a vertical axis. Indeed, there is actually a continuous distance-preserving map from the helicoid to the catenoid, describable as a complex rotation:
Obviously, a boring example of a minimal surface is the plane. Indeed, when the two circles are sufficiently separated, the catenoid is no longer optimal and a pair of disjoint discs is instead minimal.
Suppose that the circles are replaced with impenetrable discs, and we inject a prescribed volume of air into the catenoid. The requirement is no longer that the surface have zero mean curvature everywhere, but rather constant mean curvature. In this generalisation of the problem, the cylinder is optimal for a particular value of the volume.
In the simplest case, where we have a fixed volume and no constraints on the boundary, a sphere is optimal; this is why individual bubbles form spheres. It took until 2002 for this result to be extended to two volumes of air; the optimal solution is a set of three spherical films, meeting at a common circle at angles of 2π/3.
Plateau proved that all such edges between three films must be at angles of 2π/3 (c.f. this post), and vertices where four such boundaries meet must locally resemble regular tetrahedra. Together with the requirement that mean curvature must be constant on any film, we obtain Plateau’s laws.
Lord Kelvin wondered what the optimal arrangement of soap bubbles of unit volume is, so as to minimise the total surface area. He conjectured that the regular honeycomb of truncated octahedra was optimal, and for a while the Kelvin conjecture was believed to be true.
Actually, Kelvin slightly curved the faces to conform to Plateau’s laws. It transpires that there is a better polyhedral tiling giving a more optimal arrangement of soap bubbles, discovered by the Irish mathematicians Weaire and Phelan in 1994. John Conway refers to these as Scottish and Irish bubbles, and proposes a third system of Welsh bubbles. They haven’t caught on, however; the Kelvin structure occurs as the Voronoi partition of many crystal structures, and the Weaire-Phelan structure was used in the architecture of the Beijing Natural Aquatics Centre for the 2008 Olympic Games:
