Part IA of the Mathematical Tripos is marked in a rather interesting way. A naïve computation of the maximum score is 1120, although it is (in principle) possible to achieve absolutely any score (it need not even be a real number!). Firstly, let’s have a look at the scoring system:
- A long question carries 20 raw marks. A score of 15 or more results in an alpha being awarded; a score of between 10 and 14 results in a beta being awarded. A candidate can be scored on a maximum of twenty long questions.
- A short question carries 10 raw marks. A score of 8 or more results in a beta being awarded.
The alphas and betas are subsequently converted into marks according to the following scheme (quoted from the schedules of the Mathematical Tripos):
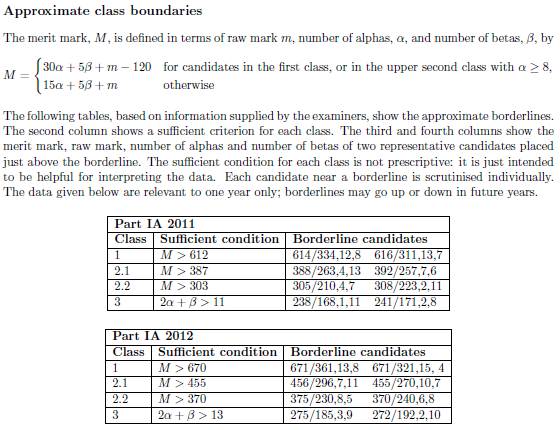
The −120 is generally referred to as an alpha tax, and cannot hurt you if you score eight or more alphas. However, if you score seven or fewer alphas and still get a first, you are actually penalised by the alpha tax. Suppose Miranda scored the following marks in 2012 (when the threshold for a first was 670):
- 10/10 on all sixteen short questions;
- 20/20 on five long questions;
- 14/20 on fifteen long questions.
Then, she would have a raw mark m = 470, together with 5 alphas and 31 betas. Now, each of the following two implications are perfectly valid:
- If Miranda achieves a 2.1 (any lower grade is impossible), then her total merit mark would be M = 470 + 15 × 5 + 5 × 31 = 700, which is sufficient for a first. Hence, Miranda achieves a first class degree.
- If Miranda achieves a first class degree, then the alpha tax would apply, and her total merit mark would be M = 470 + 30 × 5 + 5 × 31 – 120 = 655, which is insufficient for a first. Hence, Miranda achieves a 2.1.
In other words, we have a paradoxical inconsistency! Consequently, Miranda could then apply something called the Principle of Explosion, exploiting the fact that any valid proof is taken to be perfectly correct in the Tripos. Specifically, she makes the following sequence of deductions:
- By the Law of Excluded Middle, either the alpha tax applies or it does not. Let α be the proposition that the alpha tax applies. We have already established the implications that α ⇒ ¬α, and ¬α ⇒ α. Hence, both ¬α and α are true statements. Let φ be the proposition that Miranda scores 1729 on the IA Tripos. Since the logical disjunction of a true statement and an arbitrary statement is true, we have φ ∨ α. However, since ¬α is true, α is false and therefore φ must be true. Consequently, Miranda scores 1729 on Part IA of the Mathematical Tripos, thereby beating anyone who scored full marks on all questions.
Essentially, the Principle of Explosion states that if a proposition and its negation are both true, then all propositions are true. This is why it is important that axioms of set theory are consistent, as a single inconsistency would destroy mathematics.

I always used another proof for Principle of Explosion: suppose p and ¬p are both true. From latter one p is false, so p is both true and false. Take any statement q and look at p⇒q. Since p is false, this implication is trivially true. But since p is true, this implication is true iff q is true. Because we know implication is true, q also is true, Q.E.D.
Also, what would you do if ZFC turned out to be inconsistent? First thing that came to my mind is proving Riemann hypothesis, as it is definable in set theory (is it?)
I think this case is handled by the statement “The sufficient statement for each class is not prescriptive”. Your second implication is thus not valid.
That only applies to candidates very close to the borderline. In this case, it can be engineered so that Miranda is (at least) 22 marks away from the borderline for both classifications.
I think that would still be considered to be near a borderline. Perhaps you should test this yourself next year?
For IB, of course.