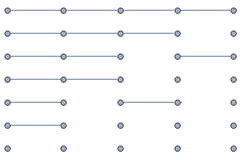
The partition numbers (sequence A000041) count the number of distinct ways to partition n identical objects. For example, p(5) = 7, as there are seven distinct ways to partition 5 objects:
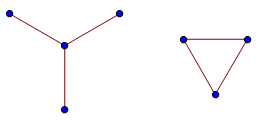
This visualisation, where partitions are graphs whose connected components are path graphs, leads to an immediately equivalent formulation as the number of distinct graphs on n vertices that do not contain the claw graph or the triangle graph as a minor.
Unlike (for example) the number of permutations, the partition numbers lack a simple closed form. Rademacher’s formula is massively complicated:
In practice, one would never use this closed form, since there are cleaner ways of computing the partition numbers. For instance, it is not too difficult to find a recursive formula for the number p(n,k) of partitions of n into at most k parts, namely:
- p(n, 1) = 1 for all
;
- p(0, k) = 1 for all
;
- p(n, k) = p(n, k − 1) + p(n − k, k) if k is not larger than n;
- p(n, k) = p(n, k − 1) otherwise.
Then, we have p(n) = p(n, n).
Generating function
Equally straightforward to determine is the generating function for the partition numbers. It is a product of the geometric series over all k, which simplifies to the reciprocal of the following product:
It is a remarkable theorem, due to Euler, that the exponents are given by generalised pentagonal numbers. In other words, this product is expressible as a simple infinite sum:
This results in a recurrence relation for the number of partitions, involving pentagonal numbers, which is much more memory-efficient than the recurrence relation involving the two-argument generalisation p(n, k).
Odd parts and distinct parts
Similar generating functions can be found for the number of partitions into odd parts, and for the number of partitions into distinct parts. One may even notice that these actually give the same generating function! This suggests that there exists a nice bijection between the partitions of n into odd parts and the partitions of n into distinct parts. There are two well-known elegant bijections:
Proof 1: Using binary
Suppose we have a partition of n into odd parts, for example 40 = 7 + 7 + 5 + 5 + 5 + 3 + 3 + 1 + 1 + 1 + 1 + 1. For each odd integer k, we count the number of parts of size k, and express it as a sum of distinct powers of two (this representation is unique). Applying it to this example gives 40 = 14 + 10 + 5 + 6 + 4 + 1, which is a sum of distinct parts. Also, this process is clearly reversible in a unique way, so we have a bijection.
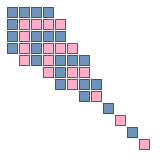
Proof 2: Using diagrams
We write each odd part as a L-shaped polyomino, and stack them together. For example, the partition 40 = 7 + 7 + 5 + 5 + 5 + 3 + 3 + 1 + 1 + 1 + 1 + 1 yields the following diagram:
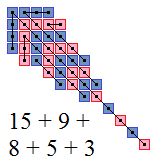
We then read off the distinct partitions as V-shaped lines, like so:
Notice that this bijection gives 40 = 15 + 9 + 8 + 5 + 3, whereas the other method gave 40 = 14 + 10 + 6 + 5 + 4 + 1. In other words, the two different proofs are really different. More interestingly, we can compose one bijection with the inverse of the other to obtain a non-trivial natural permutation of the partitions into odd/distinct parts!
Ramanujan’s congruences
Srinivasa Ramanujan discovered three surprising congruences involving the partition function:
The first congruence can be explained by defining the rank of a partition as the difference between the largest part and the number of parts, and grouping the partitions into 5 equally large sets according to the residue class of the rank (modulo 5). This also works for the second congruence, by considering ranks modulo 7. Unfortunately, residue classes of ranks modulo 11 fails spectacularly for the third congruence.
Freeman Dyson conjectured in 1944 the existence of a more sophisticated combinatorial function, the crank, such that grouping partitions according to the residue class of the crank will give equally sized subsets. It took over forty years before such a function was discovered and proved to have the desired properties. Indeed, the crank of a function also proves the other two congruences.
Congruences exist for all other primes, except for 2 and 3. Hence, we know that there are infinitely many n such that p(n) is divisible by q, for any prime q other than 2 or 3. In fact, the case q = 2 can easily be dealt with, since its falsity would imply that for all sufficiently large n, p(n) is odd. We then choose a really large N (much greater than the last n such that p(n) is even), such that the pentagonal number recurrence avoids all of the even values of p(n), and such that there are an even number of terms in the recurrence. We can do this, since the gaps between pentagonal numbers become arbitrarily large. This means that p(N) is even, leading to a blatant contradiction.
This leaves just the case of q = 3, which is an unsolved problem. It is, of course, conjectured that there are infinitely many partition numbers divisible by 3, since the negation of this statement would be incredibly bizarre. Nevertheless, it remains to be proved.

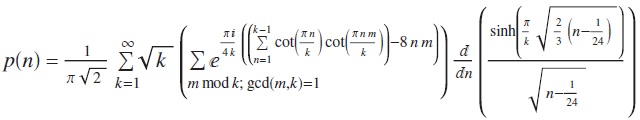
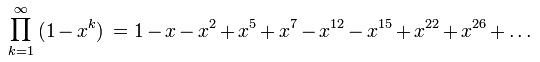
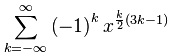
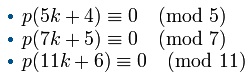
In the text near “It is a product of the geometric series”, you obviously missed some LaTeX curly braces, writing e.g.
x^(2k)
instead of
x^{(2k)}
or simply
x^{2k}
Oops! I’ve amended it now.
Pingback: Richard Elwes – Carnival of Mathematics 100
Pingback: | Partitions of N